
【题目】已知函数f(x)=(2-a)x-2(1+ln x)+a,若函数f(x)在区间![]() 上无零点,求实数a的最小值.
上无零点,求实数a的最小值.
【答案】2-4ln 2.
【解析】试题分析:
由题意可知f(x)<0在区间![]() 上恒成立不可能,则原问题等价于对x∈
上恒成立不可能,则原问题等价于对x∈![]() ,
,![]() 恒成立.构造函数
恒成立.构造函数![]() ,则
,则![]() ,
,
再令![]() ,可得m(x)> 0,则l(x)在
,可得m(x)> 0,则l(x)在![]() 上为增函数,据此可得a∈[24ln2,+∞),a的最小值为24ln2.
上为增函数,据此可得a∈[24ln2,+∞),a的最小值为24ln2.
试题解析:
函数的解析式即:![]()
![]() 为定值,而
为定值,而![]() ,
,
故f(x)<0在区间![]() 上恒成立不可能,
上恒成立不可能,
故要使函数f(x)在![]() 上无零点,
上无零点,
只要对任意的x∈![]() ,f(x)>0恒成立,
,f(x)>0恒成立,
即对x∈![]() ,
,![]() 恒成立.
恒成立.
令![]() ,则
,则![]() ,
,
再令![]() ,
,
则![]() ,故m(x)在
,故m(x)在![]() 上为减函数,于是m(x)>m(
上为减函数,于是m(x)>m(![]() )=22ln2>0,
)=22ln2>0,
从而,![]() ,于是l(x)在
,于是l(x)在![]() 上为增函数,所以l(x)<l(
上为增函数,所以l(x)<l(![]() )=24ln2,
)=24ln2,
故要使![]() 恒成立,只要a∈[24ln2,+∞),
恒成立,只要a∈[24ln2,+∞),
综上,若函数f(x)在![]() 上无零点,则a的最小值为24ln2.
上无零点,则a的最小值为24ln2.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xln x,g(x)=x3+ax2-x+2(a∈R).
(1)如果函数g(x)的单调递减区间为![]() ,求函数g(x)的解析式;
,求函数g(x)的解析式;
(2)若不等式2f(x)≤![]() +2恒成立,求实数a的取值范围.
+2恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是______(填上所有符合条件的序号)
①y=e-x在R上为增函数
②任取x>0,均有3x>2x
③函数y=f(x)的图象与直线x=a可能有两个交点
④y=2|x|的最小值为1;
⑤与y=3x的图象关于直线y=x对称的函数为y=log3x.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列{an}满足:只要ap=aq(p,q∈N*),必有ap+1=aq+1 , 则称{an}具有性质P.
(1)若{an}具有性质P,且a1=1,a2=2,a4=3,a5=2,a6+a7+a8=21,求a3;
(2)若无穷数列{bn}是等差数列,无穷数列{cn}是公比为正数的等比数列,b1=c5=1;b5=c1=81,an=bn+cn , 判断{an}是否具有性质P,并说明理由;
(3)设{bn}是无穷数列,已知an+1=bn+sinan(n∈N*),求证:“对任意a1 , {an}都具有性质P”的充要条件为“{bn}是常数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价为5元,销售单价与日均销售量的关系如图所示.
销售单价/元 | … | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | … |
日均销售量/桶 | … | 480 | 460 | 440 | 420 | 400 | 380 | … |
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为( ) 
A.9
B.18
C.20
D.35
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以O为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=2(cos θ+sin θ).
(1)求C的直角坐标方程;
(2)直线l: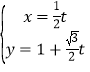 (t为参数)与曲线C交于A,B两点,与y轴交于点E,求|EA|+|EB|.
(t为参数)与曲线C交于A,B两点,与y轴交于点E,求|EA|+|EB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E的方程: ![]() ,P为椭圆上的一点(点P在第三象限上),圆P 以点P为圆心,且过椭圆的左顶点M与点C(﹣2,0),直线MP交圆P与另一点N.
,P为椭圆上的一点(点P在第三象限上),圆P 以点P为圆心,且过椭圆的左顶点M与点C(﹣2,0),直线MP交圆P与另一点N. 
(1)求圆P的标准方程;
(2)若点A在椭圆E上,求使得 ![]() 取得最小值的点A的坐标;
取得最小值的点A的坐标;
(3)若过椭圆的右顶点的直线l上存在点Q,使∠MQN为钝角,求直线l斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com