练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设不等式组 ，表示的平面区域为D，在区域D内随机取一个点，则此点到坐标原点的距离大于2的概率是（ ）
    A.
    B.
    C.
    D.

    【答案】D
    【解析】解：其构成的区域D如图所示的边长为2的正方形，面积为S1=4，

    满足到原点的距离大于2所表示的平面区域是以原点为圆心，以2为半径的圆外部，

    面积为 =4﹣π，

    ∴在区域D内随机取一个点，则此点到坐标原点的距离大于2的概率P=

    故选：D．

    【考点精析】本题主要考查了二元一次不等式（组）所表示的平面区域和几何概型的相关知识点，需要掌握不等式组表示的平面区域是各个不等式所表示的平面区域的公共部；几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】“累积净化量（CCM）”是空气净化器质量的一个重要衡量指标，它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量，以克表示．根据GB/T18801﹣2015《空气净化器》国家标准，对空气净化器的累积净化量（CCM）有如下等级划分：

    累积净化量（克）

    （3，5]

    （5，8]

    （8，12]

    12以上

    等级

    P1

    P2

    P3

    P4

    为了了解一批空气净化器（共2000台）的质量，随机抽取n台机器作为样本进行估计，已知这n台机器的
    累积净化量都分布在区间（4，14]中，按照（4，6]，（6，8]，（8，10]，（10，12]，（12，14]，均匀分组，其中累积净化量在（4，6]的所有数据有：4.5，4.6，5.2，5.7和5.9，并绘制了如下频率分布直方图．

    （Ⅰ）求n的值及频率分布直方图中的x值；
    （Ⅱ）以样本估计总体，试估计这批空气净化器（共2000台）中等级为P2的空气净化器有多少台？
    （Ⅲ）从累积净化量在（4，6]的样本中随机抽取2台，求恰好有1台等级为P2的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 存在两个极值点．
    （Ⅰ）求实数a的取值范围；
    （Ⅱ）设x1和x2分别是f（x）的两个极值点且x1＜x2 ， 证明： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列函数f（x）中，满足“x1x2∈（0，+∞）且x1≠x2有（x1﹣x2）[f（x1）﹣f（x2）]＜0”的是（ ）
    A.f（x）= ﹣x
    B.f（x）=x3
    C.f（x）=lnx+ex
    D.f（x）=﹣x2+2x

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查，统计出售价x元和销售量y杯之间的一组数据如下表所示：

    价格x

    5

    5.5

    6.5

    7

    销售量y

    12

    10

    6

    4

    通过分析，发现销售量y对奶茶的价格x具有线性相关关系．
    （Ⅰ）求销售量y对奶茶的价格x的回归直线方程；
    （Ⅱ）欲使销售量为13杯，则价格应定为多少？
    注：在回归直线y= 中， ， = ﹣ ． =146.5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某居民区随机抽取10个家庭，获得第个家庭的月收入（单位：千元）与月储蓄（单位：千元）的数据资料，算得， ，

    ，

    (1).求家庭的月储蓄对月收入的线性回归方程；

    (2).判断变量与之间的正相关还是负相关；

    (3).若该居民区某家庭月收入为7千元，预测该家庭的月储蓄.

    附：回归直线的斜率和截距的最小二乘估计公式分别为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题p：x∈R，x＋ ≥2；命题q：x0∈ ，使sin x0＋cos x0＝ ，
    则下列命题中为真命题的是( )
    A.( p)∧q
    B.p∧( q)
    C.( p)∧( q)
    D.p∧q

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直三棱柱 中，底面 是边长为2的正三角形， 是棱 的中点，且 .

    （1）试在棱 上确定一点 ，使 平面 ；
    （2）当点 在棱 中点时，求直线 与平面 所成角的大小的正弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

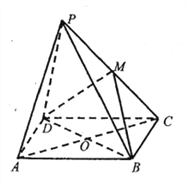
    【题目】如图，点是菱形所在平面外一点， ， 是等边三角形， ， ， 是的中点.

    （Ⅰ）求证： 平面；

    （Ⅱ）求证：平面平面；

    （Ⅲ）求直线与平面的所成角的大小.

    查看答案和解析>>

    同步练习册答案