
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,点
,点![]() 分别为
分别为![]() 的中点.
的中点.
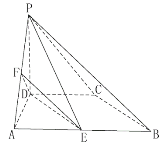
(1)求证:平面![]() 平面EFD;
平面EFD;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)详见解析(2)![]()
【解析】
(1)根据面面平行的判定定理,在面EFD内找两条相交直线平行于平面![]() ,即可证出;(2)根据等积法,
,即可证出;(2)根据等积法,![]() ,先求出三角形DEF的面积,再求出
,先求出三角形DEF的面积,再求出![]() ,即可求出点
,即可求出点![]() 到平面
到平面![]() 的距离。
的距离。
(1)由题意知:点![]() 是
是![]() 的中点,
的中点,![]() 且
且![]() ,
,
所以![]() ,所以四边形
,所以四边形![]() 是平行四边形,则
是平行四边形,则![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]()
因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]()
所以![]() 平面
平面![]() .
.
连![]() ,取
,取![]() 的中点
的中点![]() ,连
,连![]() ,易知
,易知![]() ,
,
![]() 平面
平面![]() 且
且![]() .
.
设点P到平面EFD的距离为d.
在Rt△![]() 中,
中,
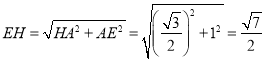
在Rt△![]() 中,
中,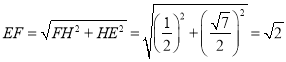
在Rt△![]() 中,
中,![]()
在Rt△![]() 中,
中,![]()
在△![]() 中,
中,![]() ,
,
即![]() ,
,
解得![]() ,
,
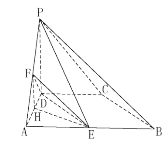
所以![]()
所以![]() .
.
因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以,
,所以,![]() 平面
平面![]() 所以,
所以,![]() 的长即是点
的长即是点![]() 到平面
到平面![]() 的距离.
的距离.
在Rt△![]() 中,
中,![]() ,
,
所以,![]() ,
,
所以![]() .
.
所以![]() ,
,
即![]() ,
,
即![]() ,解得
,解得![]() .
.
所以,点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】某省高考改革实施方案指出:该省高考考生总成绩将由语文、数学、外语3门统一高考成绩和学生自主选择的学业水平等级性考试科目共同构成.该省教育厅为了解正就读高中的学生家长对高考改革方案所持的赞成态度,随机从中抽取了100名城乡家长作为样本进行调查,调查结果显示样本中有25人持不赞成意见.下面是根据样本的调查结果绘制的等高条形图.
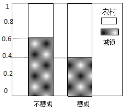
(1)根据已知条件与等高条形图完成下面的2×2列联表,并判断我们能否有95%的把握认为“赞成高考改革方案与城乡户口有关”?
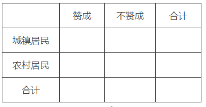
(2)利用分层抽样从持“不赞成”意见家长中抽取5名参加学校交流活动,从中选派2名家长发言,求恰好有1名城镇居民的概率.
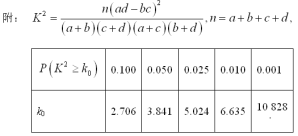
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国国际智能产业博览会(智博会)每年在重庆市举办一届,每年参加服务的志愿者分“嘉宾”、“法医”等若干小组![]() 年底,来自重庆大学、西南大学、重庆医科大学、西南政法大学的500名学生在重庆科技馆多功能厅参加了“志愿者培训”,如图是四所大学参加培训人数的不完整条形统计图,现用分层抽样的方法从中抽出50人作为2019年中国国际智博会服务的志愿者.
年底,来自重庆大学、西南大学、重庆医科大学、西南政法大学的500名学生在重庆科技馆多功能厅参加了“志愿者培训”,如图是四所大学参加培训人数的不完整条形统计图,现用分层抽样的方法从中抽出50人作为2019年中国国际智博会服务的志愿者.
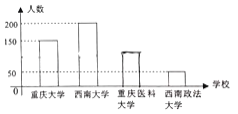
(1)若“嘉宾”小组需要2名志愿者,求这2人分别来自不同大学的概率(结果用分数表示)
(2)若“法医”小组的3名志愿者只能从重庆医科大学或西南政法大学抽出,用![]() 表示抽出志愿者来自重庆医科大学的人数,求
表示抽出志愿者来自重庆医科大学的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为实常数,函数
为实常数,函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)设![]() ,不等式
,不等式![]() 的解集为
的解集为![]() ,不等式
,不等式![]() 的解集为
的解集为![]() ,当
,当![]() 时,是否存在正整数
时,是否存在正整数![]() ,使得
,使得![]() 或
或![]() 成立.若存在,试找出所有的m;若不存在,请说明理由.
成立.若存在,试找出所有的m;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到直线
到直线![]() 的距离比到定点
的距离比到定点![]() 的距离大1.
的距离大1.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程.
的方程.
(2)若![]() 为直线
为直线![]() 上一动点,过点
上一动点,过点![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() ,
,![]() ,切点为
,切点为![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
①求证:![]() 轴;
轴;
②直线![]() 是否恒过一定点?若是,求出这个定点的坐标;若不是,请说明理由.
是否恒过一定点?若是,求出这个定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四人进行一项益智游戏,方法如下:第一步:先由四人看着平面直角坐标系中方格内的16个棋子(如图所示),甲从中记下某个棋子的坐标;第二步:甲分别告诉其他三人:告诉乙棋子的横坐标.告诉丙棋子的纵坐标,告诉丁棋子的横坐标与纵坐标相等;第三步:由乙、丙、丁依次回答.对话如下:“乙先说我无法确定.丙接着说我也无法确定.最后丁说我知道”.则甲记下的棋子的坐标为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={1,2,3,4}和集合B={1,2,3,…,n},其中n≥5,![]() .从集合A中任取三个不同的元素,其中最小的元素用S表示;从集合B中任取三个不同的元素,其中最大的元素用T表示.记X=T-S.
.从集合A中任取三个不同的元素,其中最小的元素用S表示;从集合B中任取三个不同的元素,其中最大的元素用T表示.记X=T-S.
(1)当n=5时,求随机变量X的概率分布和数学期望![]() ;
;
(2)求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com