解答:
解:(1)若a=2,则f
1(x)=e
|x-3|,f
2(x)=e
|x-2|+1,
由f
1(x)=f
2(x)得e
|x-3|=e
|x-2|+1,
即|x-3|=|x-2|+1,
若x≥3,则方程等价为x-3=x-2+1,即-3=-1,不成立,
若2<x<3,则方程等价为-x+3=x-2+1,即2x=4,解得x=2,不成立,
若x<2,则方程等价为-x+3=-x+2+1,此时恒成立;
综上使f
1(x)=f
2(x)的x的值满足x<2.
(2)即f
1(x)≤f
2(x)恒成立,得|x-2a+1|≤|x-a|+1,
即|x-2a+1|-|x-a|≤1对x∈R恒成立,
因|x-2a+1|-|x-a|≤|a-1|,
故只需|a-1|≤1,解得0≤a≤2,
又1≤a≤6,
故a的取值范围为1≤a≤2.
(3)
g(x)= | | f1(x),f1(x)≤f2(x) | | f2(x),f1(x)>f2(x). |
| |
①当1≤a≤2时,由(2)知
g(x)=f1(x)=e|x-2a+1|,
当x=2a-1∈[1,3]时,g(x)
min=1.
②当2<a≤6时,(2a-1)-a=a-1>0,
故2a-1>a.x≤a时,
f1(x)=e-x+(2a-1)>e-x+a+1=f2(x),
g(x)=f2(x)=e|x-a|+1;
x≥2a-1时,
f1(x)=ex-(2a-1)<ex-a+1=f2(x),
g(x)=f1(x)=e|x-2a+1|;
a<x<2a-1时,由
f1(x)=e-x+(2a-1)≤ex-a+1=f2(x),得
x≥,其中
a<<2a-1,
故当
≤x<2a-1时,
g(x)=f1(x)=e|x-2a+1|;
当
a<x<时,
g(x)=f2(x)=e|x-a|+1.
因此,当2<a≤6时,
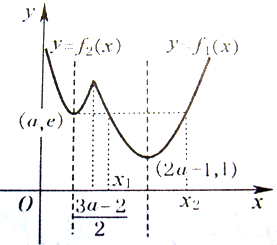
g(x)=令
f1(x)=e|x-2a+1|=e,得x
1=2a-2,x
2=2a,且
<2a-2,如图,
(ⅰ)当a≤6≤2a-2,即4≤a≤6时,g(x)
min=f
2(a)=e;
(ⅱ) 当2a-2<6≤2a-1,即
≤a<4时,
g(x)min=f1(6)=e2a-7;
(ⅲ) 当2a-1<6,即
2<a<时,g(x)
min=f
1(2a-1)=1.
综上所述,
g(x)min= | | 1,(1≤a<) | | e2a-7,(≤a<4) | | e,(4≤a≤6). |
| |
.

 解:(1)若a=2,则f1(x)=e|x-3|,f2(x)=e|x-2|+1,
解:(1)若a=2,则f1(x)=e|x-3|,f2(x)=e|x-2|+1,

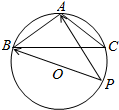 如图,在△ABC中,三内角A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,a=
如图,在△ABC中,三内角A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,a=