
【题目】在圆x2+y2﹣2x﹣6y=0内,过点E(0,1)的最长弦和最短弦之积为 .
【答案】20 ![]()
【解析】解:把圆的方程化为标准方程得:(x﹣1)2+(y﹣3)2=10,
则圆心坐标为(1,3),半径为 ![]() ,
,
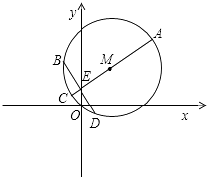
根据题意画出图象,如图所示:
由图象可知:过点E最长的弦为直径AC,最短的弦为过E与直径AC垂直的弦,则AC=2 ![]() ,MB=
,MB= ![]() ,
,
ME= ![]() =
= ![]() ,
,
所以BD=2BE=2 ![]() =2
=2 ![]() .
.
ACBD═2 ![]() =20
=20 ![]() .
.
给答案为:20 ![]() .
.
【考点精析】本题主要考查了圆的一般方程的相关知识点,需要掌握圆的一般方程的特点:(1)①x2和y2的系数相同,不等于0.②没有xy这样的二次项;(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了;(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某旅游公司为甲,乙两个旅游团提供四条不同的旅游线路,每个旅游团可任选其中一条旅游线路.
(1)求甲、乙两个旅游团所选旅游线路不同的概率;
(2)某天上午9时至10时,甲,乙两个旅游团都到同一个著名景点游览,20分钟后游览结束即离去.求两个旅游团在该著名景点相遇的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x﹣2
(Ⅰ)用定义法证明:函数f(x)在区间(﹣∞,1]上是减函数;
(Ⅱ)若函数g(x)=f(x)﹣mx是偶函数,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对应的边分别为a,b,c,且满足asinB= ![]() bcosA.
bcosA.
(1)求A的大小;
(2)若a=7,b=5,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,内角A,B,C依次成等差数列,其对边分别为a,b,c,且b= ![]() asinB.
asinB.
(1)求内角C;
(2)若b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若圆C:(x﹣5)2+(y+1)2=m(m>0)上有且只有一点到直线4x+3y﹣2=0的距离为1,则实数m的值为( )
A.4
B.16
C.4或16
D.2或4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,CD与平面ABDE所成角的正弦值为 ![]() .
.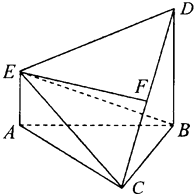
(1)若F是线段CD的中点,证明:EF⊥面DBC;
(2)求二面角D﹣EC﹣B的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1的棱长为a , M为BD1的中点,N在A1C1上,且满足|A1N|=3|NC1|.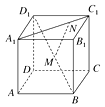
(1)求MN的长;
(2)试判断△MNC的形状.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com