
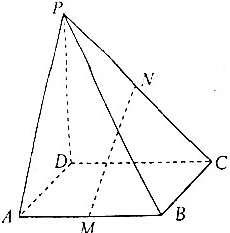
分析 (1)取CD中点Q,连结MQ,NQ.根据正方形的性质和中位线定理得出NQ∥平面PAD,NQ∥平面PAD,从而平面MNQ∥平面PAD,于是MN∥平面PAD.
(2)根据勾股定理求出NQ的长,于是PD=2NQ,代入体积公式计算.
解答  证明:(1)取CD中点Q,连结MQ,NQ.则NQ是△PCD的中位线,
证明:(1)取CD中点Q,连结MQ,NQ.则NQ是△PCD的中位线,
∴NQ∥PD,∵NQ?平面PAD,PD?平面PAD,
∴NQ∥平面PAD,
∵M是AB中点,Q是CD中点,
∴MQ∥AD,∵NQ?平面PAD,AD?平面PAD,
∴NQ∥平面PAD,
又∵NQ?平面MNQ,MQ?平面MNQ,MQ∩NQ=Q,
∴平面MNQ∥平面PAD,∵MN?平面MNQ,
∴MN∥平面PAD.
(2)∵PD⊥平面ABCD,NQ∥PD,
∴NQ⊥平面ABCD,∵MQ?平面ABCD,
∴NQ⊥MQ,又∵MQ=AD=1,∴NQ=$\sqrt{M{N}^{2}-M{Q}^{2}}$=2$\sqrt{2}$.
∴PD=2NQ=4$\sqrt{2}$.
∴V棱锥P-ABCD=$\frac{1}{3}{S}_{正方形ABCD}$•PD=$\frac{1}{3}×1×1×4\sqrt{2}$=$\frac{4\sqrt{2}}{3}$.
点评 本题考查了线面平行的判定,棱锥的体积计算,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
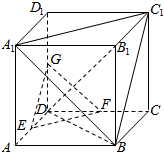 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AD、CD、DD1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AD、CD、DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k=$\frac{1}{e}$+e | |
| B. | 函数f(x)的图象在点(0,f(0))处的切线的斜率为e2-$\frac{1}{e}$ | |
| C. | 函数f(x)在[0,e]上单调递减 | |
| D. | 函数f(x)在[0,e]上的最大值为2e3+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 6 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-2i | B. | 1+2i | C. | -1-2i | D. | -1+2i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com