
 时,求圆O的半径.
时,求圆O的半径.
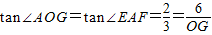 ,可得OG,再利用勾股定理可得OA=
,可得OG,再利用勾股定理可得OA=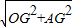 .
. 解:(1)由切割线定理PA2=PB•PC
解:(1)由切割线定理PA2=PB•PC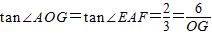 ,
,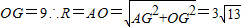
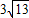 .
.

科目:高中数学 来源: 题型:
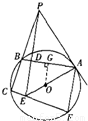
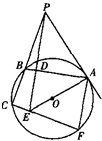 如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,PD⊥AB于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF.
如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,PD⊥AB于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF.| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源:选修设计数学A4-1人教版 人教版 题型:044
如图所示,已知PA切⊙O于A,割线PBC交⊙O于B、C,PD⊥AB于D,PD、AO的延长线相交于E,连结CE并延长交⊙O于F,连结AF.

(1)求证:△PBD∽△PEC;
(2)若AB=12,tan∠EAF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:高中数学 来源:2013届河北省高二下学期三调理科数学试卷(解析版) 题型:解答题
(本题满分12分)
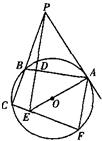
如图所示,已知PA切圆O于A,割线PBC交圆O于B、C, 于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF。
于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF。

(1)求证:B,C,E,D四点共圆;
(2)当AB=12, 时,求圆O的半径.
时,求圆O的半径.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com