
【题目】
已知![]() ,
, ![]() ,函数
,函数![]() .
.
(Ⅰ)当![]() ,
, ![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() ;
;
(Ⅱ)若函数![]() 的最大值为2,求证:
的最大值为2,求证: ![]() .
.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】试题分析:
(Ⅰ)由题意可得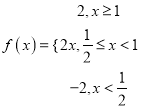 .零点分段求解不等式可得不等式的解集为
.零点分段求解不等式可得不等式的解集为![]() ;
;
(Ⅱ)由绝对值三角不等式可得![]() ,则
,则![]() .由均值不等式的结论可得
.由均值不等式的结论可得![]() ,当且仅当
,当且仅当![]() 时,等号成立.
时,等号成立.
证法二:由题意可得![]() ,零点分段可得
,零点分段可得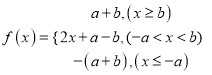 ,结合函数图像可得
,结合函数图像可得![]() .由题意结合均值不等式的结论即可证得题中的结论.
.由题意结合均值不等式的结论即可证得题中的结论.
试题解析:
(Ⅰ)当![]() 时,
时, 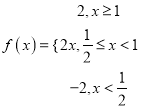 .
.
不等式![]() 为
为![]() .
.
①当![]() 时,因为不等式为
时,因为不等式为![]() ,所以不等式成立,
,所以不等式成立,
此时符合;符合要求的不等式的解集为![]() ;
;
②当![]() 时,因为不等式为
时,因为不等式为![]() ,所以
,所以![]() ,
,
此时,符合不等式的解集为![]() ;
;
③当![]() 时,因为不等式为
时,因为不等式为![]() 不成立,解集为空集;
不成立,解集为空集;
综上所述,不等式![]() 的解集为
的解集为![]() .
.
(Ⅱ)由绝对值三角不等式可得
![]() ,
, ![]() ,
, ![]()
∴![]() .
.
∴![]() ,
,
当且仅当![]() 时,等号成立.
时,等号成立.
另解:(Ⅱ)因为![]() ,
, ![]() ,所以
,所以![]() ,
,
所以函数![]()
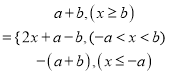 ,
,
所以函数![]() 的图象是左右两条平行于
的图象是左右两条平行于![]() 轴的射线和中间连结成的线段,
轴的射线和中间连结成的线段,
所以函数的最大值等于![]() ,所以
,所以![]() .
.
∵![]() ,
,
∴![]() .
.
或者![]()
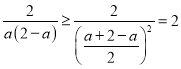 ,
,
当且仅当![]() ,即
,即![]() 时,“等号”成立.
时,“等号”成立.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
(1)当t=4,|AM|=|AN|时,求△AMN的面积;
(2)当2|AM|=|AN|时,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“中华好诗词”节目的播出,掀起了全民诵读传统诗词经典的热潮.某大学社团为调查大学生对于“中华诗词”的喜好,在该校随机抽取了40名学生,记录他们每天学习“中华诗词”的时间,并整理得到如下频率分布直方图:
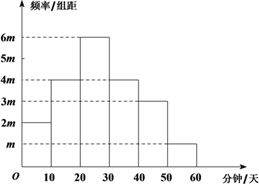
根据学生每天学习“中华诗词”的时间,可以将学生对于“中华诗词”的喜好程度分为三个等级 :
学习时间 (分钟/天) |
|
|
|
等级 | 一般 | 爱好 | 痴迷 |
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ) 从该大学的学生中随机选出一人,试估计其“爱好”中华诗词的概率;
(Ⅲ) 假设同组中的每个数据用该组区间的右端点值代替,试估计样本中40名学生每人每天学习“中华诗词”的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() ,以平面直角坐标系
,以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)将曲线![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的![]() 倍、2倍后得到曲线
倍、2倍后得到曲线![]() .试写出直线
.试写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
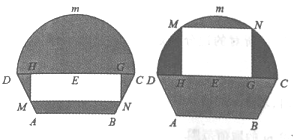
【题目】如图所示的自动通风设施.该设施的下部![]() 是等腰梯形,其中
是等腰梯形,其中![]() 为2米,梯形的高为1米,
为2米,梯形的高为1米, ![]() 为3米,上部
为3米,上部![]() 是个半圆,固定点
是个半圆,固定点![]() 为
为![]() 的中点.
的中点. ![]() 是由电脑控制可以上下滑动的伸缩横杆(横杆面积可忽略不计),且滑动过程中始终保持和
是由电脑控制可以上下滑动的伸缩横杆(横杆面积可忽略不计),且滑动过程中始终保持和![]() 平行.当
平行.当![]() 位于
位于![]() 下方和上方时,通风窗的形状均为矩形
下方和上方时,通风窗的形状均为矩形![]() (阴影部分均不通风).
(阴影部分均不通风).
(1)设![]() 与
与![]() 之间的距离为
之间的距离为![]() (
(![]() 且
且![]() )米,试将通风窗的通风面积
)米,试将通风窗的通风面积![]() (平方米)表示成关于
(平方米)表示成关于![]() 的函数
的函数![]() ;
;
(2)当![]() 与
与![]() 之间的距离为多少米时,通风窗的通风面积
之间的距离为多少米时,通风窗的通风面积![]() 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的极坐标方程为:
的极坐标方程为: ![]() .若以极点
.若以极点![]() 为原点,极轴所在直线为
为原点,极轴所在直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(Ⅰ)求圆![]() 的参数方程;
的参数方程;
(Ⅱ)在直角坐标系中,点![]() 是圆
是圆![]() 上动点,试求
上动点,试求![]() 的最大值,并求出此时点
的最大值,并求出此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有极值,且在
有极值,且在![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1)求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 的极小值为
的极小值为![]() .若存在,求出实数
.若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com