
(本题满分12分)
已知函数![]()
(1)若函数![]() 存在单调递减区间,求a的取值范围;
存在单调递减区间,求a的取值范围;
(2)当a>0时,试讨论这两个函数图象的交点个数.
(1)a>1
(2)有且仅有两个交点
(1)![]()
若使![]() 存在单调递减区间,则
存在单调递减区间,则![]() 上有解.……1分
上有解.……1分
而当![]()
问题转化为![]() 上有解,故a大于函数
上有解,故a大于函数![]() 上的最小值.
上的最小值.
………………3分
又![]() 上的最小值为-1,所以a>1.……4分
上的最小值为-1,所以a>1.……4分
(2)令![]()
函数![]() 的交点个数即为函数
的交点个数即为函数![]() 的零点的个数.……5分
的零点的个数.……5分
![]()
令![]() 解得
解得![]()
随着x的变化,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
| - | 0 | + |
|
| 单调递减 | 极(最)小值2+lna | 单调递增 |
…………7分
①当![]() 恒大于0,函数
恒大于0,函数![]() 无零点.……8分
无零点.……8分
②当![]() 由上表,函数
由上表,函数![]() 有且仅有一个零点.
有且仅有一个零点.
……9分
③![]() 显然
显然![]()
![]() 内单调递减,
内单调递减,
所以![]() 内有且仅有一个零点 …………10分
内有且仅有一个零点 …………10分
当![]()
由指数函数![]() 与幂函数
与幂函数![]() 增长速度的快慢,知存在
增长速度的快慢,知存在![]()
使得![]()
从而![]()
因而![]()
又![]() 内单调递增,
内单调递增,![]() 上的图象是连续不断的曲线,
上的图象是连续不断的曲线,
所以![]() 内有且仅有一个零点. …………11分
内有且仅有一个零点. …………11分
因此,![]() 有且仅有两个零点.
有且仅有两个零点.
综上,![]() 的图象无交点;当
的图象无交点;当![]() 的图象有且仅有一个交点;
的图象有且仅有一个交点;![]() 的图像有且仅有两个交点.……12分
的图像有且仅有两个交点.……12分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海市金山区高三上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分12分,第1小题6分,第2小题6分)
已知集合A={x| | x–a | < 2,xÎR
},B={x|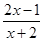 <1,xÎR }.
<1,xÎR }.
(1) 求A、B;
(2) 若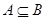 ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省高三10月月考理科数学试卷(解析版) 题型:解答题
(本题满分12分)
设函数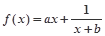 (
(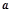 ,
,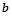 为常数),且方程
为常数),且方程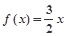 有两个实根为
有两个实根为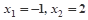 .
.
(1)求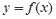 的解析式;
的解析式;
(2)证明:曲线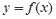 的图像是一个中心对称图形,并求其对称中心.
的图像是一个中心对称图形,并求其对称中心.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三第二次月考文科数学 题型:解答题
(本题满分12分,(Ⅰ)小问4分,(Ⅱ)小问6分,(Ⅲ)小问2分.)
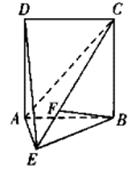
如图所示,直二面角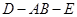 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
,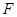 为
为 上的点,且
上的点,且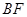 ⊥平面
⊥平面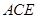
(Ⅰ)求证: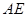 ⊥平面
⊥平面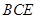
(Ⅱ)求二面角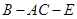 的大小;
的大小;
(Ⅲ)求点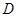 到平面
到平面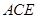 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com