
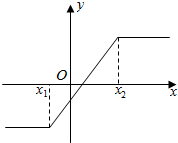
 对任意的x1<0<x2,若函数f(x)=a|x-x1|+b|x-x2|的图象为如图所示的一条折线(两侧的射线均平行于x轴),则实数a、b应满足的条件是( )
对任意的x1<0<x2,若函数f(x)=a|x-x1|+b|x-x2|的图象为如图所示的一条折线(两侧的射线均平行于x轴),则实数a、b应满足的条件是( )| A. | a+b=0且a-b>0 | B. | a+b=0且a-b<0 | C. | a-b=0且a+b>0 | D. | a-b=0且a+b<0. |
分析 将f(x)化为分段函数,逐段与图象对应,根据图象在各段上的变化规律:常数函数、正比例函数、常数函数确定解析式的各项系数.找出共同条件.
解答 解:当x≤x1时,f(x)=-a(x-x1)-b(x-x2)=-(a+b)x+(ax1+bx2) 由图可知$\left\{\begin{array}{l}{a+b=0,①}\\{a{x}_{1}+b{x}_{2}<0,②}\end{array}\right.$
当x1<0<x2时,f(x)=a(x-x1)-b(x-x2)=(a-b)x-ax1+bx2 由图可知$\left\{\begin{array}{l}{a-b>0,①′}\\{-a{x}_{1}+b{x}_{2}=0,②′}\end{array}\right.$
当x≥x2时,f(x)=a(x-x1)+b(x-x2)=(a+b)x-(ax1+bx2) 由图又可得出①②两式.
由 ①,①′两式可得a=-b>0,同时使得②,②′成立.
故实数a、b应满足的条件是:a>0且a+b=0 (或a=-b>0),
故选:A.
点评 本题考查绝对值函数的图象,以及识图能力、逆向思维能力.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $8\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,c>b,则a>c | B. | 若a>-b,则c-a<c+b | ||
| C. | 若a>b,则ac2>bc2 | D. | 若a>b,c>d,则ac>bd |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,在△ADE翻折的过程中,有下列命题:
如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,在△ADE翻折的过程中,有下列命题:| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com