Question

以下命题正确的为（　　）

A．有两个相邻的侧面是矩形的棱柱是直棱柱

B．有一个侧面是矩形的棱柱是直棱柱

C．底面是正多形的棱锥是正棱锥

D．正棱锥各侧面与底面所成的二面角不一定都相等

Answer 1

分析：根据直棱柱的定义，结合直线与平面垂直的判定定理，可以证明出A项是正确的．再分别说明其它各项的错误原因：根据直棱柱的定义与性质，举出反例可以说明B项是错误的；根据正棱锥的定义，举出反可以例说明C项是错误的；最后根据正棱锥的定义与性质，可证出各侧面与底面所成角的正弦相等，从而得到各侧面与底面所成的二面角相等，所以
D项错误．

解答：解：对于A，如图，设四棱锥ABCD-A₁B₁C₁D₁中，若侧面ABB₁A₁和BCC₁B₁都矩形，则
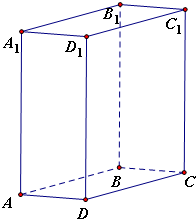
∵BB₁⊥AB，BB₁⊥CB，AB∩BC=B，AB、BC?底面ABCD
∴BB₁⊥底面ABCD
可得四棱柱ABCD-A₁B₁C₁D₁是直棱柱，故A正确；
对于B，如果棱柱只有一个侧面是矩形，而其它的侧面不是矩形，
则这个棱柱就不是直棱柱，故B错误；
对于C，若棱锥底面是正多形，但顶点在底面的射影不是底面正多边形的中心，则不符合正棱锥的定义，因此这个棱锥不是正棱锥，故C错误；
对于D，若一个棱锥是正棱锥，则它的底面是正多边形，且顶点在底面的射影是底面正多边形的中心，
作出正棱锥一个侧面等腰三角形的高，
则这个侧面与底面所成角的正弦值等于正棱锥的高与侧面等腰三角形的高的比值，
由于正棱锥各个侧面是全等的等腰三角形，所以各侧面与底面所成角的正弦相等，
因为各侧面与底面所成的二面角是锐角，故正棱锥各侧面与底面所成的二面角相等
故D错误．
故选A

点评：本题以命题真假的判断与应用为载体，着重考查了直棱柱、正棱锥的定义与性质，考查了基本概念的理解与空间想象力，属于基础题．