
【题目】已知函数f(x)=ex﹣ax2(a∈R).
(1)若g(x)= ![]() 有三个极值点x1 , x2 , x,求a的取值范围;
有三个极值点x1 , x2 , x,求a的取值范围;
(2)若f(x)≥﹣ax3+1对任意x∈[0,1]都恒成立的a的最大值为μ,证明:5 ![]() .
.
【答案】
(1)解:g(x)= ![]() ,定义域为(﹣∞,﹣1)∪(﹣1,+∞),
,定义域为(﹣∞,﹣1)∪(﹣1,+∞),
g′(x)= ![]() ,∵g′(0)=0,
,∵g′(0)=0,
只需h(x)=ex﹣ax﹣2a=0应有两个既不等于0也不等于﹣1的根,h′(x)=ex﹣a,
①当a≤0时,h′(x)>0,∴h(x)单增,h(x)=0最多只有一个实根,不满足;
②当a>0时,h′(x)=ex﹣a=0x=lna,
当x∈(﹣∞,lna)时,h′(x)<0,h(x)单减;
当x∈(lna,+∞)时,h'(x)>0,h(x)单增;∴h(x0)是h(x)的极小值,
而x→+∞时,h(x)→+∞,x→﹣∞时,h(x)→+∞,
要h(x)=0有两根,只需h(lna)<0,
由h(lna)=elna﹣alna﹣2a<0﹣alna﹣a<0lna>﹣1a> ![]()
又由h(0)=1﹣2a≠0a≠ ![]() ,
,
反之,若a ![]() a
a ![]() 且时,则h(﹣1)=
且时,则h(﹣1)= ![]() ,h(x)=0的两根中,一个大于﹣1,另一个小于﹣1.
,h(x)=0的两根中,一个大于﹣1,另一个小于﹣1.
在定义域中,连同x=0,g′(x)=0共有三个相异实根,
且在三根的左右,g′(x)正负异号,它们是g(x)的三个极值点.
综上,a的取值范围为( ![]() ,
, ![]() )
) ![]()
(2)证明: f(x)≥﹣ax3+1对任意x∈[0,1]都恒成立
ex﹣ax2≥﹣ax3+1ex﹣1≥a(x2﹣x3)对x∈[0,1]恒成立,
①当x=0或1时,a∈R均满足;
②ex﹣1≥a(x2﹣x3)对x∈(0,1)恒成立a≤ ![]() 对x∈(0,1)恒成立,
对x∈(0,1)恒成立,
记u(x)= ![]() ,x∈(0,1),则(a)max=μ=(
,x∈(0,1),则(a)max=μ=( ![]() )min,x∈(0,1),
)min,x∈(0,1),
欲证5 ![]() 5<(
5<( ![]() )min<
)min< ![]() ,
,
而 ![]() ,
,
只需证明 ![]() ,显然成立.
,显然成立.
下证: ![]() ,
,
先证: ![]() ,
, ![]() ,
,
令 ![]() ,
, ![]() ,
,
∴v'(x)在(0,1)上单增,v″(x)>v″(0)=0,
∴v'(x)在(0,1)上单增,∴v′(x)>v′(0)=0,∴v′(x)在(0,1)上单增,
∴v(x)>v(0)=1,即证.
要证:ex>5x2﹣5x3+1,x∈(0,1),
只需证1+x+ ![]() +
+ ![]() ≥5x2﹣5x3+1,x(0,1)
≥5x2﹣5x3+1,x(0,1) ![]()
31x3﹣27x2+6x≥0x(31x2﹣27x+6)≥031x2﹣27x+6≥0,x∈(0,1)
而△=272﹣4×31×6=﹣15<0,开口向上,上不等式恒成立,从而得证命题成立
【解析】1、由已知求导可得h′(x)=ex﹣a,利用导数可求出函数的极值,进而得到h(x0)是h(x)的极小值。
2、利用导数求闭区间上函数的最值。
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值,以及对函数的最大(小)值与导数的理解,了解求函数
是极小值,以及对函数的最大(小)值与导数的理解,了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D= ![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.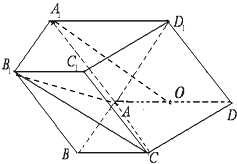
(Ⅰ)求证:A1O∥平面AB1C;
(Ⅱ)求锐二面角A﹣C1D1﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2016年1月1日起,我国全面二孩政策正式实施,这次人口与生育政策的历史性调整,使得“要不要再生一个”“生二孩能休多久产假”等成为千千万万个家庭在生育决策上避不开的话题.为了解针对产假的不同安排方案形成的生育意愿,某调查机构随机抽取了200户有生育二胎能力的适龄家庭进行问卷调查,得到如下数据:
产假安排(单位:周) | 14 | 15 | 16 | 17 | 18 |
有生育意愿家庭数 | 4 | 8 | 16 | 20 | 26 |
(1)若用表中数据所得的频率代替概率,面对产假为14周与16周,估计某家庭有生育意愿的概率分别为多少?
(2)假设从5种不同安排方案中,随机抽取2种不同安排分别作为备选方案,然后由单位根据单位情况自主选择.
①求两种安排方案休假周数和不低于32周的概率;
②如果用ξ表示两种方案休假周数和.求随机变量ξ的分布及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|y= ![]() },集合B={x|y=lg(﹣x2﹣7x﹣12)},集合C={x|m+1≤x≤2m﹣1}.
},集合B={x|y=lg(﹣x2﹣7x﹣12)},集合C={x|m+1≤x≤2m﹣1}.
(1)求A∩B;
(2)若A∪C=A,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,M、N分别是棱AB、CC1的中点,△MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题:
①平面MB1P⊥ND1;②平面MB1P⊥平面ND1A1;③△MB1P在底面ABCD上的射影图形的面积为定值;④△MB1P在侧面D1C1CD上的射影图形是三角形.
其中正确命题的序号是 . 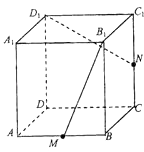
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,且cos2B+3cos(A+C)+2=0, ![]() ,那么△ABC周长的最大值是( )
,那么△ABC周长的最大值是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景点拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为36米,其中大圆弧所在圆的半径为14米,设小圆弧所在圆的半径为x米,圆心角为θ(弧度).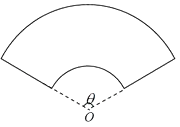
(1)求θ关于x的函数关系式;
(2)已知对花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为16元/米,设花坛的面积与装饰总费用之比为y,求y关于x的函数关系式,并求出y的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com