
【题目】已知函数f(x)= ![]() +3lnax﹣x,g(x)=xex+cosx(a≠0).
+3lnax﹣x,g(x)=xex+cosx(a≠0).
(1)求函数y=f(x)的单调区间;
(2)若x1∈[1,2],x2∈[0,3],使得f( ![]() )>g(x2)成立,求实数a的取值范围.
)>g(x2)成立,求实数a的取值范围.
【答案】
(1)解:依题知,a>0时,x>0;a<0时,x<0,
∵ ![]() ,
,
令f'(x)>0,解得1<x<2;令f'(x)<0,解得x<1,或x>2,
故当a>0时,f(x)在(1,2)上为增函数,在(0,1)、(2,+∞)上为减函数;
a<0时,f(x)在(﹣∞,0)上为减函数.
(2)解:x1∈[1,2],x2∈[0,3],
使得f(x1)>g(x2)成立,
f(x)在[1,2]上的最大值大于g(x)在[0,3]的最小值,
由(Ⅰ)知,a>0,且f(x)max=f(2)=3ln2a﹣1,
又g'(x)=ex+xex﹣sinx>0在[0,3]恒成立,即g(x)在[0,3]上单调递增,
有g(x)min=g(0)=1,
故依题得3ln2a﹣1>1,
解得: ![]() .
.
【解析】(1)求出f(x)的导数,解关于导函数的不等式,求出函数的单调区间即可;(2)问题转化为f(x)在[1,2]上的最大值大于g(x)在[0,3]的最小值,分别求出其最大值和最小值得到关于a的不等式,解出即可.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查 结果如下表所示:
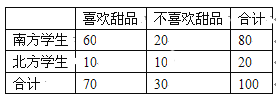
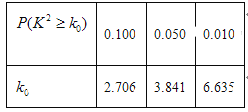
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
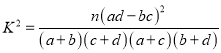 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x),满足当x>0时,f(x)>1,且对任意的x,y∈R,有f(x+y)=f(x)f(y),f(1)=2.
(1)求f(0)的值;
(2)求证:对任意x∈R,都有f(x)>0;
(3)解不等式f(3﹣2x)>4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2为椭圆C: ![]() =1(a>b>0)的左右焦点,O是坐标原点,过F2作垂直于x轴的直线MF2交椭圆于M,设|MF2|=d.
=1(a>b>0)的左右焦点,O是坐标原点,过F2作垂直于x轴的直线MF2交椭圆于M,设|MF2|=d.
(1)证明:b2=ad;
(2)若M的坐标为( ![]() ,1),求椭圆C的方程.
,1),求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作样本,如图是样本的茎叶图,规定:成绩不低于120分时为优秀成绩. 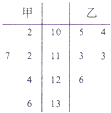
(1)从甲班的样本中有放回的随机抽取2个数据,求其中只有一个优秀成绩的概率;
(2)从甲、乙两个班级的样本中分别抽取2名学生的成绩,记获优秀成绩的总人数为X,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地建一座桥,两端的桥墩已建好,这两墩相距m米,余下的工程只需要建两端桥墩之间的桥面和桥墩.经预测一个桥墩的工程费用为256万元,距离为x米的相邻两墩之间的桥面工程费用为(2+ ![]() )x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.假设需要新建n个桥墩.
)x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.假设需要新建n个桥墩.
(1)写出n关于x的函数关系式;
(2)写出y关于x的函数关系式;
(3)当m=640米时,需新建多少个桥墩才能使y最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com