
分析 (1)f(x)在区间(0,+∞)上单调递增,等价于f′(x)=ex-2kx≥0(x>0)恒成立,分k≤0,0<k≤$\frac{1}{2}$,k>$\frac{1}{2}$三种情况进行讨论,前两种情况易作出判断,k>$\frac{1}{2}$时,利用导数求出最值解不等式即可;
(2)①k=$\frac{1}{2}$时,利用导数可判断f(x)在(0,+∞)上单调递增,从而可得f(x)>f(0)=1;
②由(1)知,对于x∈(0,+∞),有f(x)=ex>$\frac{1}{2}$x2+1,则e2x>2x2+1,ln(2x2+1)<2x,从而有ln($\frac{2}{{n}^{4}}$+1)<$\frac{2}{{n}^{2}}$(n∈N*),从而证出结论.
解答 解:(1)f′(x)=ex-2kx,下求使f′(x)≥0(x>0)恒成立的k的取值范围.
若k≤0,显然f′(x)>0,f(x)在区间(0,+∞)上单调递增;
记φ(x)=ex-2kx,则φ′(x)=ex-2k,
当0<k≤$\frac{1}{2}$时,∵ex>e0=1,2k≤1,∴φ′(x)>0,则φ(x)在(0,+∞)上单调递增,
于是f′(x)=φ(x)>φ(0)=1>0,∴f(x)在(0,+∞)上单调递增;
当k>$\frac{1}{2}$时,φ(x)=ex-2kx在(0,ln2k)上单调递减,在(ln2k,+∞)上单调递增,
于是f′(x)=φ(x)≥φ(ln2k)=eln2k-2kln2k,
由eln2k-2kln2k≥0,得2k-2kln2k≥0,则$\frac{1}{2}$≤k≤$\frac{e}{2}$,
综上,k的取值范围为(-∞,$\frac{e}{2}$].
(2)①f(x)=ex-$\frac{1}{2}$x2,则h(x)=f′(x)=ex-x,
∴h′(x)=ex-1>0(x>0),
∴h(x)=f′(x)在(0,+∞)上递增,∴f′(x)>f′(0)=1>0,
∴f(x)=ex-$\frac{1}{2}$x2在(0,+∞)上单调递增,
故f(x)>f(0)=1.
②由①知,对于x∈(0,+∞),有f(x)=ex>$\frac{1}{2}$x2+1,∴e2x>2x2+1,
则ln(2x2+1)<2x,从而有ln($\frac{2}{{n}^{4}}$+1)<$\frac{2}{{n}^{2}}$(n∈N*),
于是:ln($\frac{2}{{1}^{4}}$+1)+ln($\frac{2}{{2}^{4}}$+1)+ln($\frac{2}{{3}^{4}}$+1)+…+ln($\frac{2}{{n}^{4}}$+1)
<$\frac{2}{{1}^{2}}$+…+$\frac{2}{{n}^{2}}$<$\frac{2}{{1}^{2}}$+$\frac{2}{1×2}$+…+$\frac{2}{(n-1)×n}$
=2+2(1-$\frac{1}{2}$+…+$\frac{1}{n-1}$-$\frac{1}{n}$)
=4-$\frac{2}{n}$<4,
故:($\frac{2}{{1}^{4}}$+1)($\frac{2}{{2}^{4}}$+1)($\frac{2}{{3}^{4}}$+1)…($\frac{2}{{n}^{4}}$+1)<e4.
点评 本题考查利用导数研究函数的单调性、最值及不等式证明等知识,考查学生综合运用知识分析问题解决问题的能力,综合性较强,对能力要求很高.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届安徽淮北十二中高三上月考二数学(理)试卷(解析版) 题型:解答题
已知命题 关于
关于 的方程
的方程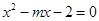 在
在 有解,命题
有解,命题 在
在 单调递增;若
单调递增;若 为真命题,
为真命题, 是真命题,求实数
是真命题,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com