
【题目】如图,直线l:y=x+b (b>0),抛物线C:y2=2px(p>0),已知点P(2,2)在抛物线C上,且抛物线C上的点到直线l的距离的最小值为![]() .
.
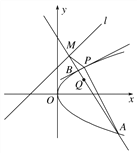
(1)求直线l及抛物线C的方程;
(2)过点Q(2,1)的任一直线(不经过点P)与抛物线C交于A,B两点,直线AB与直线l相交于点M,记直线PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在实数λ,使得k1+k2=λk3?若存在,试求出λ的值;若不存在,请说明理由.
【答案】(1)直线l的方程为y=x+2,抛物线C的方程为y2=2x.;(2)存在,且![]() 2.
2.
【解析】试题分析:(1)设出直线方程,联立直线和抛物线的方程,得到关于![]() 的一元二次方程,利用根与系数的关系和点到直线的距离公式进行求解;(2)设出直线方程,联立直线和抛物线的方程,得到关于
的一元二次方程,利用根与系数的关系和点到直线的距离公式进行求解;(2)设出直线方程,联立直线和抛物线的方程,得到关于![]() 的一元二次方程,利用根与系数的关系得到等量关系,再联立两直线方程得到另一等量关系,两者结合即可证明.
的一元二次方程,利用根与系数的关系得到等量关系,再联立两直线方程得到另一等量关系,两者结合即可证明.
试题解析:(1)∵点P(2,2)在抛物线C上,∴p=1.
设与直线l平行且与抛物线C相切的直线l′的方程为y=x+m,
由![]()
得x2+(2m-2)x+m2=0,Δ=(2m-2)2-4m2=4-8m,
由Δ=0,得m=![]() ,
,
则直线l′的方程为y=x+![]() .
.
两直线l,l′间的距离即为抛物线C上的点到直线l的最短距离,
有![]() =
=![]() ,
,
解得b=2或b=-1(舍去).
∴直线l的方程为y=x+2,抛物线C的方程为y2=2x.
(2)∵直线AB的斜率存在,且k≠0,
∴设直线AB的方程为y-1=k(x-2)(k≠0),
即y=kx-2k+1.
联立![]()
得ky2-2y-4k+2=0(k≠0),
设点A,B的坐标分别为A(x1,y1),B(x2,y2),
则y1+y2=![]() (k≠0),y1y2=
(k≠0),y1y2=![]() (k≠0).
(k≠0).
∵k1=![]() =
=![]() =
=![]() ,k2=
,k2=![]() ,
,
∴k1+k2=![]() +
+![]()
=![]()
= =
=![]() (k≠0).
(k≠0).
联立![]()
得xM=![]() ,yM=
,yM=![]() ,
,
∴k3=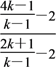 =
=![]() ,
,
∴k1+k2=2k3.
∴存在实数λ,使得k1+k2=λk3成立,且λ=2.


科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=3,且an+1﹣3an=3n,(n∈N*),数列{bn}满足bn=3﹣nan.
(1)求证:数列{bn}是等差数列;
(2)设![]() ,求满足不等式
,求满足不等式![]() 的所有正整数n的值.
的所有正整数n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=sin2ax-![]() sin ax·cos ax-
sin ax·cos ax-![]() (a>0)的图象与直线y=b相切,并且切点的横坐标依次成公差为
(a>0)的图象与直线y=b相切,并且切点的横坐标依次成公差为![]() 的等差数列.
的等差数列.
(1)求a,b的值;
(2)若x0∈![]() ,且x0是y=f(x)的零点,试写出函数y=f(x)在
,且x0是y=f(x)的零点,试写出函数y=f(x)在![]() 上的单调增区间.
上的单调增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com