
【题目】已知函数![]() .
.
(1)若函数![]() 在定义域上是单调增函数,求实数a的取值范围;
在定义域上是单调增函数,求实数a的取值范围;
(2)讨论![]() 的极值点的个数;
的极值点的个数;
(3)若![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 的极值点的个数为0;当
的极值点的个数为0;当![]() 时,
时,![]() 的极值点的个数为2;(3)
的极值点的个数为2;(3)![]()
【解析】
(1)求出导函数![]() ,题意说明
,题意说明![]() 在
在![]() 上恒成立,可用分离参数法转化为求函数最值(可用基本不等式求最值).
上恒成立,可用分离参数法转化为求函数最值(可用基本不等式求最值).
(2)由![]() ,对
,对![]() 分类讨论,在(1)的基础上,
分类讨论,在(1)的基础上,![]() 时无极值点,在
时无极值点,在![]() 时,求出
时,求出![]() 的两根,可列表得出
的两根,可列表得出![]() 的正负,得
的正负,得![]() 的单调性,从而得极值点.
的单调性,从而得极值点.
(3)由(2)知![]() ,
,![]() ,求出
,求出![]() ,注意
,注意![]() 代换后可转化为
代换后可转化为![]() 的代数式,令
的代数式,令![]() ,首先有
,首先有![]() ,
,![]() 变为
变为![]() 的函数,由
的函数,由![]() 求出
求出![]() 的取值范围后可得
的取值范围后可得![]() 的取值范围.
的取值范围.
解:(1)定义域为![]() ,由题意得
,由题意得![]()
因为函数![]() 在定义域上是单调增函数,所以
在定义域上是单调增函数,所以![]() 在
在![]() 上恒成立
上恒成立
因为![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上恒成立
上恒成立
因为![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
所以![]() ,即
,即![]() ,所以,实数a的取值范围为
,所以,实数a的取值范围为![]()
(2)![]() ,
,
①![]() 时,由第(1)问可知,函数
时,由第(1)问可知,函数![]() 在定义域上是单调增函数;
在定义域上是单调增函数;
所以![]() 无极值点,即
无极值点,即![]() 的极值点的个数为0
的极值点的个数为0
②![]() 时,令
时,令![]() ,得:
,得:![]() ,
,![]()
当![]() 时,
时,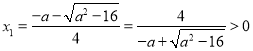 ,故
,故![]()
列表:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
|
| 极大值 |
| 极小值 |
|
当![]() 时,
时,![]() 有极大值,当
有极大值,当![]() 时,
时,![]() 有极小值
有极小值
所以,![]() 的极值点的个数为2
的极值点的个数为2
综上所述,当![]() 时,
时,![]() 的极值点的个数为0;当
的极值点的个数为0;当![]() 时,
时,![]() 的极值点的个数为2
的极值点的个数为2
(3)由题意知,![]() ,
,
因为![]() 是函数
是函数![]() 的两个极值点,所以是方程
的两个极值点,所以是方程![]() 的两个不等实根
的两个不等实根
所以![]() ,
,![]()
所以![]()
![]()
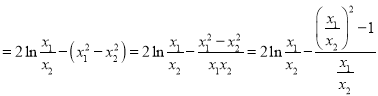
令![]() ,记
,记![]()
由![]() 可得:
可得:![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以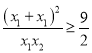 ,所以
,所以![]() ,即
,即![]() ,
,
因为![]() ,解得:
,解得:![]()
又![]() ,所以
,所以![]() 在
在![]() 上单调减
上单调减
所以![]()
所以![]() 的最小值为
的最小值为![]()


科目:高中数学 来源: 题型:
【题目】总体由编号为01,02,03,![]() ,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )
,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )
78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
A. 05 B. 09 C. 07 D. 20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() 函数
函数![]() .
.
(1)将函数![]() 的图像向右平移m(
的图像向右平移m(![]() )个单位长度,所得图像对应的函数为奇函数,写出m的最小值(不要求写过程);
)个单位长度,所得图像对应的函数为奇函数,写出m的最小值(不要求写过程);
(2)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若函数![]() (
(![]() )在区间
)在区间![]() 上是单调递增函数,求正数
上是单调递增函数,求正数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在R上的奇函数,且满足
是定义在R上的奇函数,且满足![]() ,
,![]() =1,数列{
=1,数列{![]() }满足
}满足![]() =﹣1,
=﹣1, ![]() (
(![]() ),其中
),其中![]() 是数列{
是数列{![]() }的前n项和,则
}的前n项和,则![]() =
=
A. ﹣2 B. ﹣1 C. 0 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() :
:![]() =0(a>0),曲线
=0(a>0),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系;
为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系;
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)已知极坐标方程为![]() =
=![]() 的直线与曲线
的直线与曲线![]() ,
,![]() 分别相交于P,Q两点(均异于原点O),若|PQ|=
分别相交于P,Q两点(均异于原点O),若|PQ|=![]() ﹣1,求实数a的值;
﹣1,求实数a的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 同时满足:①对于定义域上的任意
同时满足:①对于定义域上的任意![]() ,恒有
,恒有![]() ;②对于定义域上的任意
;②对于定义域上的任意![]() ,当
,当![]() 时,恒有
时,恒有![]() ,则称函数
,则称函数![]() 为“理想函数”.给出下列四个函数中:①
为“理想函数”.给出下列四个函数中:① ![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④ 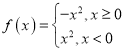 ,能被称为“理想函数”的有_____(请将所有正确命题的序号都填上).
,能被称为“理想函数”的有_____(请将所有正确命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(1)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(2)在上述样本中,学校从成绩为![]() 的学生中随机抽取
的学生中随机抽取![]() 人进行学习交流,求这
人进行学习交流,求这![]() 人来自同一个班级的概率.
人来自同一个班级的概率.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
(1)若函数![]() 在区间
在区间![]() 上的最小值为1,求实数m的值;
上的最小值为1,求实数m的值;
(2)若函数![]() ,其中
,其中![]() 为奇函数,
为奇函数,![]() 为偶函数,不等式
为偶函数,不等式![]() 对任意
对任意![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com