解:(1)∵实数x,y满足:e
x+y=x+1,变形,得x+y=ln(x+1),
∴y=ln(x+1)-x,
又∵y=f(x)∴f(x)=ln(x+1)-x,(x>-1)
则
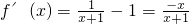
当-1<x<0时,f'(x)>0;
当x>0时,f'(x)<0
∴f(x)在(-1,0)上单调递增;在(0,+∞)上单调递减.
(2)
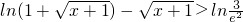
变形为
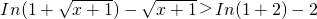
∵f(x)=ln(x+1)-x,
∴不等式
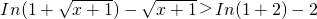
等价于f(

)>f(2)
由(1)知f(x)=ln(1+x)-x在(0,+∞)上单调递减
∴f(

)>f(2)等价于

<2
解得-1<x<2
∴不等式
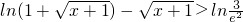
解集为 {x|-1<x<2}
分析:(1)先根据式子e
x+y=x+1把y用x表示,就可得到函数y=f(x)的解析式,求导数,因为导数大于0,得到的x的范围是函数的增区间,导数小于0,得到的x的范围是函数的减区间,所以只需判断在函数定义域中何时导数大于0,何时导数小于0,就可求出函数的单调区间.
(2)先把要解的不等式
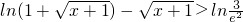
变形为
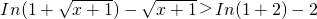
,不等号的左右两边分别是函数f(x)=ln(x+1)-x当自变量为

和2时的函数值,再根据f(x)的单调性就可解出不等式.
点评:本题(1)考察了导数与函数的单调性的关系,导数大于0,函数为增函数,导数小于0,函数为减函数.
(2)考查了利用函数的单调性解不等式,关键是把不等式的左右两边都化为含函数符号的式子.

 .
.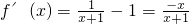
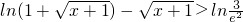 变形为
变形为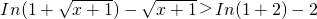
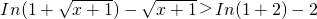 等价于f(
等价于f( )>f(2)
)>f(2) )>f(2)等价于
)>f(2)等价于 <2
<2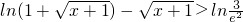 解集为 {x|-1<x<2}
解集为 {x|-1<x<2}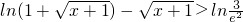 变形为
变形为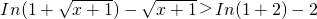 ,不等号的左右两边分别是函数f(x)=ln(x+1)-x当自变量为
,不等号的左右两边分别是函数f(x)=ln(x+1)-x当自变量为 和2时的函数值,再根据f(x)的单调性就可解出不等式.
和2时的函数值,再根据f(x)的单调性就可解出不等式.
