
ЎҫМвДҝЎҝНЁ№эЛж»ъСҜОК110ГыРФұрІ»Н¬өДЦРС§ЙъКЗ·с°®әГФЛ¶ҜЈ¬өГөҪИзПВөДБРБӘұнЈә
ДР | Е® | ЧЬјЖ | |
°®әГ | 40 | 20 | 60 |
І»°®әГ | 20 | 30 | 50 |
ЧЬјЖ | 60 | 50 | 110 |
УЙ![]() өГЈ¬
өГЈ¬![]()
| 0Ј®050 | 0Ј®010 | 0Ј®001 |
| 3Ј®841 | 6Ј®635 | 10Ј®828 |
ІОХХёҪұнЈ¬өГөҪөДХэИ·ҪбВЫКЗ ЈЁ Ј©
A. ФЪ·ёҙнОуөДёЕВКІ»і¬№э0.001өДЗ°МбПВЈ¬ИПОӘЎ°°®әГФЛ¶ҜУлРФұрУР№ШЎұ
B. ФЪ·ёҙнОуөДёЕВКІ»і¬№э0.01өДЗ°МбПВЈ¬ИПОӘ Ў°°®әГФЛ¶ҜУлРФұрУР№ШЎұ
C. ФЪ·ёҙнОуөДёЕВКІ»і¬№э0.001өДЗ°МбПВЈ¬ИПОӘЎ°°®әГФЛ¶ҜУлРФұрОЮ№ШЎұ
D. УР![]() ТФЙПөД°СОХИПОӘЎ°°®әГФЛ¶ҜУлРФұрОЮ№ШЎұ
ТФЙПөД°СОХИПОӘЎ°°®әГФЛ¶ҜУлРФұрОЮ№ШЎұ

| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘ4ГыС§ЙъәН2ГыҪМКҰХҫФЪТ»ЕЕХХПаЈ¬ЗуЈә
ЈЁ1Ј©ЦРјд¶юёцО»ЦГЕЕҪМКҰЈ¬УР¶аЙЩЦЦЕЕ·ЁЈҝ
ЈЁ2Ј©КЧОІІ»ЕЕҪМКҰЈ¬УР¶аЙЩЦЦЕЕ·ЁЈҝ
ЈЁ3Ј©БҪГыҪМКҰІ»ХҫФЪБҪ¶ЛЈ¬ЗТұШРлПаБЪЈ¬УР¶аЙЩЦЦЕЕ·ЁЈҝ
ЈЁ4Ј©БҪГыҪМКҰІ»ДЬПаБЪөДЕЕ·ЁУР¶аЙЩЦЦЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОӘБЛЖА№АAЈ¬BБҪјТҝмөЭ№«ЛҫөД·юОсЦКБҝЈ¬ҙУБҪјТ№«ЛҫөДҝН»§ЦРёчЛж»ъійИЎ100ГыҝН»§ЧчОӘСщұҫЈ¬ҪшРР·юОсЦКБҝВъТв¶ИөчІйЈ¬Ҫ«AЈ¬BБҪ№«ЛҫөДөчІйөГ·Ц·Цұр»жЦЖіЙЖөВК·ЦІјұнәНЖөВК·ЦІјЦұ·ҪНјЈ®№ж¶Ё![]() ·ЦТФПВОӘ¶ФёГ№«Лҫ·юОсЦКБҝІ»ВъТвЈ®
·ЦТФПВОӘ¶ФёГ№«Лҫ·юОсЦКБҝІ»ВъТвЈ®
·ЦЧй | ЖөКэ | ЖөВК |
|
|
|
|
|
|
|
| 0.4 |
|
|
|
|
|
|
әПјЖ |
|
|

ЈЁўсЈ©ЗуСщұҫЦР¶ФB№«ЛҫөД·юОсЦКБҝІ»ВъТвөДҝН»§ИЛКэЈ»
ЈЁўтЈ©ПЦҙУСщұҫ¶ФAЈ¬BБҪёц№«Лҫ·юОсЦКБҝІ»ВъТвөДҝН»§ЦРЈ¬Лж»ъійИЎ2ГыҪшРРЧЯ·ГЈ¬ЗуХвБҪГыҝН»§¶јАҙЧФУЪB№«ЛҫөДёЕВКЈ»
ЈЁўуЈ©ёщҫЭСщұҫКэҫЭЈ¬КФ¶ФБҪёц№«ЛҫөД·юОсЦКБҝҪшРРЖАјЫЈ¬ІўІыКцАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЙиfЈЁxЈ©=4cosЈЁҰШx©Ғ ![]() Ј©sinҰШx©ҒcosЈЁ2ҰШx+ҰРЈ©Ј¬ЖдЦРҰШЈҫ0Ј®
Ј©sinҰШx©ҒcosЈЁ2ҰШx+ҰРЈ©Ј¬ЖдЦРҰШЈҫ0Ј®
ЈЁ1Ј©ЗуәҜКэy=fЈЁxЈ©өДЦөУт
ЈЁ2Ј©ИфfЈЁxЈ©ФЪЗшјд ![]() ЙПОӘФцәҜКэЈ¬ЗуҰШөДЧоҙуЦөЈ®
ЙПОӘФцәҜКэЈ¬ЗуҰШөДЧоҙуЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЛДАвЧ¶![]() ЦРЈ¬өЧГж
ЦРЈ¬өЧГж![]() КЗХэ·ҪРОЈ¬ІаГж
КЗХэ·ҪРОЈ¬ІаГж![]() ЎНөЧГж
ЎНөЧГж![]() Ј¬Иф
Ј¬Иф![]() ·ЦұрОӘ
·ЦұрОӘ![]() өДЦРөгЈ®
өДЦРөгЈ®
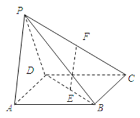
ЈЁўсЈ©ЗуЦӨЈә![]() ЖҪГж
ЖҪГж![]() Ј»
Ј»
ЈЁўтЈ©ЗуЦӨЈәЖҪГж![]() ЎНЖҪГж
ЎНЖҪГж![]() Ј®
Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ¶ЁТеФЪ![]() ЙПөДәҜКэ
ЙПөДәҜКэ![]() ВъЧг
ВъЧг![]() .өұ
.өұ![]() КұЈ¬
КұЈ¬![]() Ј¬өұ
Ј¬өұ![]() КұЈ¬
КұЈ¬![]() ,ФтfЈЁ1Ј©+fЈЁ2Ј©+Ўӯ+fЈЁ2015Ј©=ЈЁ Ј©
,ФтfЈЁ1Ј©+fЈЁ2Ј©+Ўӯ+fЈЁ2015Ј©=ЈЁ Ј©
A. 333 B. 336 C. 1678 D. 2015
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЙиaЎКRЈ¬ИфxЈҫ0КұҫщУР[ЈЁa©Ғ1Ј©x©Ғ1]ЈЁx2©Ғax©Ғ1Ј©ЎЭ0Ј¬Фтa= Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіЙМіЎҫӯУӘТ»ЕъҪшјЫКЗ30ФӘ/јюөДЙМЖ·Ј¬ФЪКРіЎКФПъЦР·ўПЦЈ¬ҙЛЙМЖ·ПъКЫјЫ![]() ФӘУлИХПъКЫБҝ
ФӘУлИХПъКЫБҝ![]() јюЦ®јдУРИзПВ№ШПөЈә
јюЦ®јдУРИзПВ№ШПөЈә
x | 45 | 50 |
y | 27 | 12 |
ЈЁ1Ј©И·¶Ё![]() Ул
Ул![]() өДТ»ёцТ»ҙОәҜКэ№ШПөКҪ
өДТ»ёцТ»ҙОәҜКэ№ШПөКҪ![]() Ј»
Ј»
ЈЁ2Ј©ИфИХПъКЫАыИуОӘPФӘЈ¬ёщҫЭЈЁЈЙЈ©ЦР№ШПөРҙіцP№ШУЪ![]() өДәҜКэ№ШПөЈ¬ІўЦёіцөұПъКЫөҘјЫОӘ¶аЙЩФӘКұЈ¬ІЕДЬ»сөГЧоҙуөДИХПъКЫАыИуЈҝ
өДәҜКэ№ШПөЈ¬ІўЦёіцөұПъКЫөҘјЫОӘ¶аЙЩФӘКұЈ¬ІЕДЬ»сөГЧоҙуөДИХПъКЫАыИуЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ОӘЧФИ»¶ФКэөДөЧКэ.
ОӘЧФИ»¶ФКэөДөЧКэ.
ЈЁўсЈ©ИфәҜКэ![]() ФЪ
ФЪ![]() ЙПҙжФЪБгөгЈ¬ЗуКөКэ
ЙПҙжФЪБгөгЈ¬ЗуКөКэ![]() өДИЎЦө·¶О§Ј»
өДИЎЦө·¶О§Ј»
ЈЁўтЈ©ИфәҜКэ![]() ФЪ
ФЪ![]() ҙҰөДЗРПЯ·ҪіМОӘ
ҙҰөДЗРПЯ·ҪіМОӘ![]() .ЗуЦӨЈә¶ФИОТвөД
.ЗуЦӨЈә¶ФИОТвөД![]() Ј¬ЧЬУР
Ј¬ЧЬУР![]() .
.
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com