
分析 (1)根据图象的平移即可得到函数的解析式,
(2)方法一,采取分离参数,转化为$k=\frac{{2|{x-1}|+1}}{x^2}$在x∈[1,3]上有解或者$k=\frac{{2|{x-1}|+1}}{x^2}$在$x∈[{\frac{1}{2},1})$上有解,根据函数的性质即可求出k的范围
方法二,采用根的分布,原题等价于kx2-2(x-1)-1=0在x∈[1,3]上有解或者kx2-2(1-x)-1=0在$x∈[{\frac{1}{2},1}]$上有解,分别根据根与系数的关系即可求出k的范围.
解答 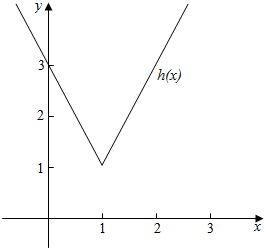 解:(1)由图象的平移,h(x)=2|x-1|+1
解:(1)由图象的平移,h(x)=2|x-1|+1
(2)解:函数y=h(x)的图象与函数g(x)=kx2的图象在$x∈[{\frac{1}{2},3}]$上至少 有一个交点,等价于h(x)-g(x)=0在$x∈[{\frac{1}{2},3}]$上有解,
有一个交点,等价于h(x)-g(x)=0在$x∈[{\frac{1}{2},3}]$上有解,
即2|x-1|+1-kx2=0在$x∈[{\frac{1}{2},3}]$上有解,
解法一:用分离参数处理:kx2=2|x-1|+1在$x∈[{\frac{1}{2},3}]$上有解,$k=\frac{{2|{x-1}|+1}}{x^2}$在$x∈[{\frac{1}{2},3}]$上有解,
等价于$k=\frac{{2|{x-1}|+1}}{x^2}$在x∈[1,3]上有解或者$k=\frac{{2|{x-1}|+1}}{x^2}$在$x∈[{\frac{1}{2},1})$上有解,
因为$k=\frac{{2({x-1})+1}}{x^2}=-\frac{1}{x^2}+\frac{2}{x}=-{({\frac{1}{x}-1})^2}+1,因为\frac{1}{x}∈[{\frac{1}{3},1}],所以k∈[{\frac{5}{9},1}]$$k=\frac{{2({1-x})+1}}{x^2}=\frac{3}{x^2}-\frac{2}{x}=3{({\frac{1}{x}-\frac{1}{3}})^2}-\frac{1}{3},因为\frac{1}{x}∈({1,2}]所以k∈[{1,8}]$
综上,$k∈[{\frac{5}{9},8}]$.
解法二:用实根分布:
原题等价于kx2-2(x-1)-1=0在x∈[1,3]上有解或者kx2-2(1-x)-1=0在$x∈[{\frac{1}{2},1}]$上有解,
(1)kx2-2(x-1)-1=0在x∈[1,3]上有解
令g(x)=kx2-2(x-1)-1,k=0时显然无解.
当k<0时,$g(1)•g(3)≤0⇒\frac{5}{9}≤k≤1$(舍)
当k>0,$g(1)•g(3)≤0⇒\frac{5}{9}≤k≤1$或者$\left\{{\begin{array}{l}{1≤\frac{1}{k}≤3}\\{△=4-4k≥0⇒k=1}\\{g(1)≥0}\\{g(3)≥0}\end{array}}\right.⇒k=1$
所以$\frac{5}{9}≤k≤1$
(2)kx2-2(1-x)-1=0在$x∈[{\frac{1}{2},1}]$上有解:
令h(x)=kx2+2x-3,k=0时显然无解.
当k>0时,$h(1)•h({\frac{1}{2}})≤0⇒1≤k≤8$,所以1≤k≤8
当k<0时,$h(1)•h({\frac{1}{2}})≤0⇒1≤k≤8$(舍)或者$\left\{{\begin{array}{l}{\frac{1}{2}≤-\frac{1}{k}≤1}\\{△=4+12k≥0⇒k∈∅}\\{h(1)≤0}\\{h({\frac{1}{2}})≤0}\end{array}}\right.$
所以1≤k≤8
综上,$k∈[{\frac{5}{9},8}]$.
点评 本题考查了函数解析式的求法和根的分布问题,关键是分类讨论,考查学生分析解决问题的能力,属于中档题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{1,\sqrt{2}}]$ | B. | [2,4] | C. | $[{\sqrt{2},2}]$ | D. | $[{1,\sqrt{3}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2800元 | B. | 3000元 | C. | 3800元 | D. | 3818元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充分不必要条件 | D. | 必要不充分条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com