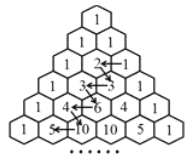
[题目]杨辉三角.是二项式系数在三角形中的一种几何排列.在欧洲.这个表叫做帕斯卡三角形.帕斯卡(1623--1662)是在1654年发现这一规律的.比杨辉要迟年.比贾宪迟年.如图的表在我国南宋数学家杨辉1261年所著的一书里就出现了.这又是我国数学史上的一个伟大成就.如图所示.在“杨辉三角中.从1开始箭头所指的数组成一个锯齿形数列:.则此数列前项和为 . 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】杨辉三角，是二项式系数在三角形中的一种几何排列。在欧洲，这个表叫做帕斯卡三角形。帕斯卡（1623——1662）是在1654年发现这一规律的，比杨辉要迟年，比贾宪迟年。如图的表在我国南宋数学家杨辉1261年所著的《详解九章算法》一书里就出现了，这又是我国数学史上的一个伟大成就。如图所示，在“杨辉三角”中，从1开始箭头所指的数组成一个锯齿形数列：，则此数列前项和为________.

【答案】164

【解析】

分别考查每行第二个数和第三个数组成的数列，然后求和两次即可求得最终结果。

考查每行第二个数组成的数列：，归纳推理可知其通项公式为，其前项和；

每行第三个数组成的数列：，

归纳推理可知其通项公式为，

其前8项和，

据此可得题中数列前项和为.

故答案为：164

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如果对一切实数x、y，不等式 ﹣cos2x≥asinx﹣ 恒成立，则实数a的取值范围是（）
A.（﹣∞， ]
B.[3，+∞）
C.[﹣2 ，2 ]
D.[﹣3，3]

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设是不小于3的正整数，集合，对于集合中任意两个元素，.

定义1：.

定义2：若，则称，互为相反元素，记作，或.

（Ⅰ）若，，，试写出，，以及的值；

（Ⅱ）若，证明：；

（Ⅲ）设是小于的正奇数，至少含有两个元素的集合，且对于集合中任意两个不相同的元素，，都有，试求集合中元素个数的所有可能值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆C： + =1（a＞b＞0）的焦点为F1 ， F2 ，离心率为，点P为其上动点，且三角形PF1F2的面积最大值为，O为坐标原点．
（1）求椭圆C的方程；
（2）若点M，N为C上的两个动点，求常数m，使 =m时，点O到直线MN的距离为定值，求这个定值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】△ABC中，角A，B，C的对边分别为a，b，c，且三角形的面积S= accosB．
（1）求角B的大小；
（2）若a=2 ，点D在AB的延长线上，且AD=3，cos∠ADC= ，求b的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知空间四边形ABCD中，AB=BD=AD=2，BC=1，CD= ，若二面角A﹣BD﹣C的取值范围为[ ， ]，则该几何体的外接球表面积的取值范围为．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】牛顿法求方程f（x）=0近似根原理如下：求函数y=f（x）在点（xn ， f（xn））处的切线y=f′（xn）（x﹣xn）+f（xn），其与x轴交点横坐标xn+1=xn﹣ （n∈N*），则xn+1比xn更靠近f（x）=0的根，现已知f（x）=x2﹣3，求f（x）=0的一个根的程序框图如图所示，则输出的结果为（）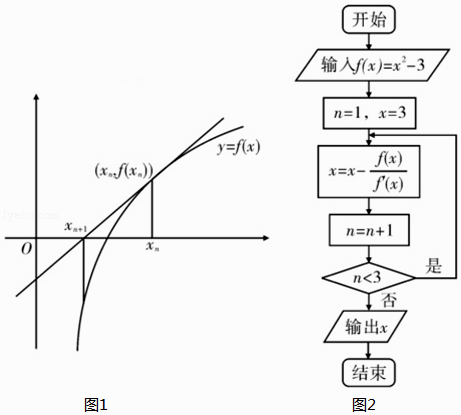
A.2
B.1.75
C.1.732
D.1.73