
【题目】[选修4-4:极坐标与参数方程]
在直角坐标系xOy中,直线l的参数方程为 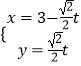 (t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位),且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4sinθ.
(t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位),且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4sinθ.
(1)求圆C的直角坐标方程和直线l普通方程;
(2)设圆C与直线l交于点A,B,若点P的坐标为(3,0),求|PA|+|PB|.
科目:高中数学 来源: 题型:
【题目】已知过原点的动直线![]() 与圆
与圆![]()
![]() 相交于不同的两点
相交于不同的两点![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]()
![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B是椭圆 ![]() =1和双曲线
=1和双曲线 ![]() =1的公共顶点,其中a>b>0,P是双曲线上的动点,M是椭圆上的动点(P,M都异于A,B),且满足
=1的公共顶点,其中a>b>0,P是双曲线上的动点,M是椭圆上的动点(P,M都异于A,B),且满足 ![]() =λ(
=λ( ![]() )(λ∈R),设直线AP,BP,AM,BM的斜率分别为k1 , k2 , k3 , k4 , 若k1+k2=
)(λ∈R),设直线AP,BP,AM,BM的斜率分别为k1 , k2 , k3 , k4 , 若k1+k2= ![]() ,则k3+k4= .
,则k3+k4= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若命题p:从有2件正品和2件次品的产品中任选2件得到都是正品的概率为三分之一;命题q:在边长为4的正方形ABCD内任取一点M,则∠AMB>90°的概率为 ![]() ,则下列命题是真命题的是( )
,则下列命题是真命题的是( )
A.p∧q
B.(p)∧q
C.p∧(q)
D.q
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响,我校随机抽取100名学生,对学习成绩和学案使用程度进行了调查,统计数据如表所示:
善于使用学案 | 不善于使用学案 | 总计 | |
学习成绩优秀 | 40 | ||
学习成绩一般 | 30 | ||
总计 | 100 |
参考公式: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
已知随机抽查这100名学生中的一名学生,抽到善于使用学案的学生概率是0.6.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法分析:有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
(3)利用分层抽样的方法从善于使用学案的同学中随机抽取6人,从这6人中抽出3人继续调查,设抽出学习成绩优秀的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了给贫困山区的孩子们赶制一批爱心电子产品,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下表所示:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 |
| 3 | 4 |
|
经统计发现零件个数![]() 与加工时间
与加工时间![]() 具有线性相关关系.
具有线性相关关系.
(1)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)试预测加工10个零件需要多少时间.
利用公式: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程|x2﹣2x﹣1|﹣t=0有四个不同的实数根x1、x2、x3、x4,且x1<x2<x3<x4 , 则2(x4﹣x1)+(x3﹣x2)的取值范围是( )
A.(8,6 ![]() )
)
B.(6 ![]() ,4
,4 ![]() )
)
C.[8,4 ![]() ]
]
D.(8,4 ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
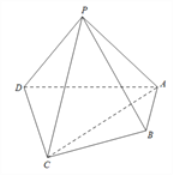
【题目】如图,在四棱锥![]() 中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,
中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2, ![]() .
.
(1)求证:PD⊥平面PAB;
(2)求直线PB与平面PCD所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com