
【题目】如图,设椭圆 ![]() +
+ ![]() =1(a>b>0)的左右焦点分别为F1 , F2 , 点D在椭圆上,DF1⊥F1F2 ,
=1(a>b>0)的左右焦点分别为F1 , F2 , 点D在椭圆上,DF1⊥F1F2 , ![]() =2
=2 ![]() ,△DF1F2的面积为
,△DF1F2的面积为 ![]() . (Ⅰ)求该椭圆的标准方程;
. (Ⅰ)求该椭圆的标准方程;
(Ⅱ)是否存在圆心在y轴上的圆,使圆在x轴的上方与椭圆有两个交点,且圆在这两个交点处的两条切线互相垂直并分别过不同的焦点?若存在,求出圆的方程;若不存在,请说明理由.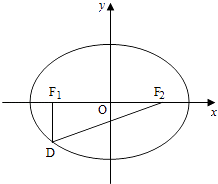
【答案】解:(Ⅰ)设F1(﹣c,0),F2(c,0),其中c2=a2﹣b2 , 由 ![]() =2
=2 ![]() ,得|DF1|=
,得|DF1|= ![]() =
= ![]() c,
c,
从而 ![]() =
= ![]() |DF1||F1F2|=
|DF1||F1F2|= ![]() c2=
c2= ![]() ,故c=1.
,故c=1.
从而|DF1|= ![]() ,由DF1⊥F1F2 , 得
,由DF1⊥F1F2 , 得 ![]() =
= ![]() +
+ ![]() =
= ![]() ,
,
因此|DF2|= ![]() ,
,
所以2a=|DF1|+|DF2|=2 ![]() ,故a=
,故a= ![]() ,b2=a2﹣c2=1,
,b2=a2﹣c2=1,
因此,所求椭圆的标准方程为 ![]() +y2=1;
+y2=1;
(Ⅱ)设圆心在y轴上的圆C与椭圆 ![]() +y2=1相交,P1(x1 , y1),P2(x2 , y2)是两个交点,
+y2=1相交,P1(x1 , y1),P2(x2 , y2)是两个交点,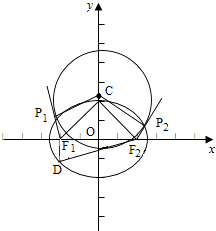
y1>0,y2>0,F1P1 , F2P2是圆C的切线,且F1P1⊥F2P2 , 由圆和椭圆的对称性,易知x2=﹣x1 , y1=y2 , |P1P2|=2|x1|,
由(Ⅰ)知F1(﹣1,0),F2(1,0),所以 ![]() =(x1+1,y1),
=(x1+1,y1), ![]() =(﹣x1﹣1,y1),再由F1P1⊥F2P2 , 得﹣
=(﹣x1﹣1,y1),再由F1P1⊥F2P2 , 得﹣ ![]() +
+ ![]() =0,
=0,
由椭圆方程得1﹣ ![]() =
= ![]() ,即3
,即3 ![]() +4x1=0,解得x1=﹣
+4x1=0,解得x1=﹣ ![]() 或x1=0.
或x1=0.
当x1=0时,P1 , P2重合,此时题设要求的圆不存在;
当x1=﹣ ![]() 时,过P1 , P2 , 分别与F1P1 , F2P2垂直的直线的交点即为圆心C,设C(0,y0)
时,过P1 , P2 , 分别与F1P1 , F2P2垂直的直线的交点即为圆心C,设C(0,y0)
由F1P1 , F2P2是圆C的切线,知CP1⊥F1P1 , 得 ![]()
![]() =﹣1,而|y1|=|x1+1|=
=﹣1,而|y1|=|x1+1|= ![]() ,
,
故y0= ![]() ,
,
故圆C的半径|CP1|= 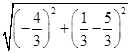 =
= ![]() .
.
综上,存在满足题设条件的圆,其方程为x2+ ![]() =
= ![]()
【解析】(Ⅰ)设F1(﹣c,0),F2(c,0),依题意,可求得c=1,易求得|DF1|= ![]() =
= ![]() ,|DF2|=
,|DF2|= ![]() ,从而可得2a=2
,从而可得2a=2 ![]() ,于是可求得椭圆的标准方程;(Ⅱ)设圆心在y轴上的圆C与椭圆
,于是可求得椭圆的标准方程;(Ⅱ)设圆心在y轴上的圆C与椭圆 ![]() +y2=1相交,P1(x1 , y1),P2(x2 , y2)是两个交点,依题意,利用圆和椭圆的对称性,易知x2=﹣x1 , y1=y2 , |P1P2|=2|x1|,由F1P1⊥F2P2 , 得x1=﹣
+y2=1相交,P1(x1 , y1),P2(x2 , y2)是两个交点,依题意,利用圆和椭圆的对称性,易知x2=﹣x1 , y1=y2 , |P1P2|=2|x1|,由F1P1⊥F2P2 , 得x1=﹣ ![]() 或x1=0,分类讨论即可求得圆心及半径,从而可得的方程.
或x1=0,分类讨论即可求得圆心及半径,从而可得的方程.


科目:高中数学 来源: 题型:
【题目】已知各项均不相等的等差数列{an}的前四项和S4=14,且a1 , a3 , a7成等比数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Tn为数列{ ![]() }的前n项和,若Tn≤λan+1对n∈N*恒成立,求实数λ的最小值.
}的前n项和,若Tn≤λan+1对n∈N*恒成立,求实数λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在亚丁湾海域执行护航任务的中国海军“徐州”舰,在A处收到某商船在航行中发出求救信号后,立即测出该商船在方位角方位角(是从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角)为45°、距离A处为10 n mile的C处,并测得该船正沿方位角为105°的方向,以9 n mile/h的速度航行,“徐州”舰立即以21 n mile/h的速度航行前去营救.
(1)“徐州”舰最少需要多少时间才能靠近商船?
(2)在营救时间最少的前提下,“徐州”舰应按照怎样的航行方向前进?(角度精确到0.1°,时间精确到1min,参考数据:sin68.2°≈0.9286)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,b= ![]() sinB,且满足tanA+tanC=
sinB,且满足tanA+tanC= ![]() . (Ⅰ)求角C和边c的大小;
. (Ⅰ)求角C和边c的大小;
(Ⅱ)求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系![]() 中,曲线
中,曲线![]() 的方程是
的方程是![]() ,直线
,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx+x(x﹣a)2(a∈R),若存在 ![]() ,使得f(x)>xf'(x)成立,则实数a的取值范围是( )
,使得f(x)>xf'(x)成立,则实数a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=![]() ,O为AC与BD的交点,E为棱PB上一点.
,O为AC与BD的交点,E为棱PB上一点.

(1)证明:平面EAC⊥平面PBD;
(2)若PD∥平面EAC,求三棱锥P-EAD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:  ,其中
,其中![]() 是仪器的月产量.(注:总收益=总成本+利润)
是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润![]() 表示为月产量
表示为月产量![]() 的函数;
的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com