
【题目】若数列![]() 满足:对任意
满足:对任意![]() ,都有
,都有![]() ,则称
,则称![]() 为“紧密”数列.
为“紧密”数列.
(1)设某个数列为“紧密”数列,其前![]() 项依次为
项依次为![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若数列![]() 的前项和
的前项和![]() ,判断
,判断![]() 是否为“紧密”数列,并说明理由;
是否为“紧密”数列,并说明理由;
(3)设![]() 是公比为
是公比为![]() 的等比数列,前
的等比数列,前![]() 项和为
项和为![]() ,且
,且![]() 与
与![]() 均为“紧密”数列,求实数
均为“紧密”数列,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 是 “紧密”数列,理由见详解;(3)
是 “紧密”数列,理由见详解;(3)![]()
【解析】
(1)根据题意,得到![]() ,且
,且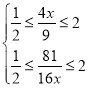 ,求解,即可得出结果;
,求解,即可得出结果;
(2)根据![]() ,求出
,求出![]() ,计算
,计算![]() 的范围,即可得出结论;
的范围,即可得出结论;
(3)先讨论![]() ,易得满足题意;再讨论
,易得满足题意;再讨论![]() ,得到
,得到![]() ,
,![]() ,根据
,根据![]() 为“紧密”数列,得到
为“紧密”数列,得到![]() 或
或![]() ,分别根据这两种情况,计算
,分别根据这两种情况,计算![]() 的范围,即可得出结果.
的范围,即可得出结果.
(1)若数列![]() 为“紧密”数列,则
为“紧密”数列,则![]() ,且
,且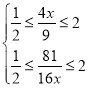 ,解得:
,解得:![]() ;
;
即![]() 的取值范围为
的取值范围为![]() ;
;
(2)数列![]() 为“紧密”数列;理由如下:
为“紧密”数列;理由如下:
数列![]() 的前项和
的前项和![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
又![]() ,即
,即![]() 满足
满足![]() ,
,
因此![]()
![]() ,
,
所以对任意![]() ,
,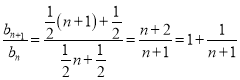 ,
,
所以![]() ,
,
因此数列![]() 为“紧密”数列;
为“紧密”数列;
(3)因为数列![]() 是公比为
是公比为![]() 的等比数列,前
的等比数列,前![]() 项和为
项和为![]() ,
,
当![]() 时,有
时,有![]() ,
,![]() ,
,
所以![]() ,
,![]() ,满足题意;
,满足题意;
当![]() 时,
时,![]() ,
,![]() ,因为
,因为![]() 为“紧密”数列,
为“紧密”数列,
所以![]() ,即
,即![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
,
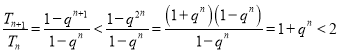 ,
,
所以![]() ,满足
,满足![]() 为“紧密”数列;
为“紧密”数列;
当![]() 时,
时,![]() ,不满足
,不满足![]() 为“紧密”数列;
为“紧密”数列;
综上,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】以直角坐标系xOy的坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程是![]() ,曲线C2的参数方程是
,曲线C2的参数方程是![]() (θ为参数).
(θ为参数).
(1)写出曲线C1,C2的普通方程;
(2)设曲线C1与y轴相交于A,B两点,点P为曲线C2上任一点,求|PA|2+|PB|2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
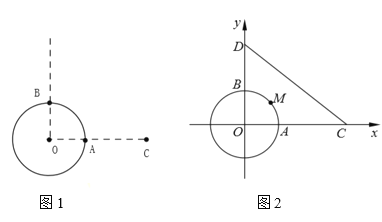
【题目】如图1,点![]() 为半径为
为半径为![]() 千米的圆形海岛的最东端,点
千米的圆形海岛的最东端,点![]() 为最北端,在点
为最北端,在点![]() 的正东
的正东![]() 千米
千米![]() 处停泊着一艘缉私艇,某刻,发现在
处停泊着一艘缉私艇,某刻,发现在![]() 处有一小船正以速度
处有一小船正以速度![]() (千米/小时)向正北方向行驶,已知缉私艇的速度为
(千米/小时)向正北方向行驶,已知缉私艇的速度为![]() (千米/小时) .
(千米/小时) .
(1)为了在最短的时间内拦截小船检查,缉私艇应向什么方向行驶? (精确到![]() )
)
(2)海岛上有一快艇要为缉私艇送去给养,问选择海岛边缘的哪一点![]() 出发才能行程最短? (如图2建立坐标系, 用坐标表示点
出发才能行程最短? (如图2建立坐标系, 用坐标表示点![]() 的位置)
的位置)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接2019年全国文明城市评比,某市文明办对市民进行了一次文明创建知识的网络问卷调查.每一位市民有且仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如下表所示:
组别 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,文明办为此次参加问卷调查的市民制定如下奖励方案:
(i)得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
(ii)每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;
;
②若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂销售部以箱为单位销售某种零件,每箱的定价为![]() 元,低于
元,低于![]() 箱按原价销售,不低于
箱按原价销售,不低于![]() 箱则有以下两种优惠方案:①以
箱则有以下两种优惠方案:①以![]() 箱为基准,每多
箱为基准,每多![]() 箱送
箱送![]() 箱;②通过双方议价,买方能以优惠
箱;②通过双方议价,买方能以优惠![]() 成交的概率为
成交的概率为![]() ,以优惠
,以优惠![]() 成交的概率为
成交的概率为![]() .
.
![]() 甲、乙两单位都要在该厂购买
甲、乙两单位都要在该厂购买![]() 箱这种零件,两单位都选择方案②,且各自达成的成交价格相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;
箱这种零件,两单位都选择方案②,且各自达成的成交价格相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;
![]() 某单位需要这种零件
某单位需要这种零件![]() 箱,以购买总价的数学期望为决策依据,试问该单位选择哪种优惠方案更划算?
箱,以购买总价的数学期望为决策依据,试问该单位选择哪种优惠方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列说法中正确的有( )
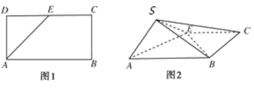
①存在点E使得直线SA⊥平面SBC;
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行;
④存在点E使得SE⊥BA.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com