
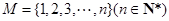 ,若集合
,若集合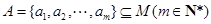 ,且对任意的
,且对任意的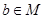 ,存在
,存在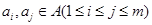 ,使得
,使得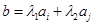 (其中
(其中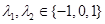 ),则称集合
),则称集合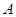 为集合
为集合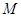 的一个
的一个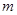 元基底.
元基底.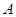 是否为集合
是否为集合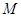 的一个二元基底,并说明理由;
的一个二元基底,并说明理由;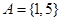 ,
,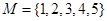 ;
;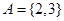 ,
,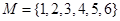 .
.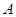 是集合
是集合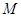 的一个
的一个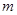 元基底,证明:
元基底,证明: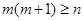 ;
;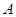 为集合
为集合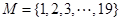 的一个
的一个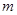 元基底,求出
元基底,求出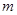 的最小可能值,并写出当
的最小可能值,并写出当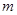 取最小值时
取最小值时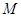 的一个基底
的一个基底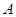 .
.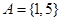 不是
不是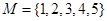 的一个二元基底.
的一个二元基底. ;
;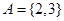 是
是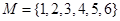 的一个二元基底.
的一个二元基底.  ,
, . 3分
. 3分 ,则
,则
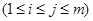 的正整数共有
的正整数共有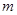 个;
个;
 的正整数共有
的正整数共有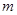 个;
个;
 的正整数至多有
的正整数至多有 个;
个;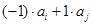
 的正整数至多有
的正整数至多有 个.
个. 含
含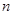 个不同的正整数,
个不同的正整数,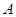 为集合
为集合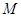 的一个
的一个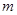 元基底.
元基底. ,即
,即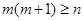 . 8分
. 8分 ,所以
,所以 .
. 时,
时, ,即用基底中元素表示出的数最多重复一个. *
,即用基底中元素表示出的数最多重复一个. * 为
为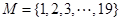 的一个4元基底,
的一个4元基底, ,则
,则 .
. 时,有
时,有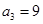 ,这时
,这时 或
或 .
. ,则由
,则由 ,与结论*矛盾.
,与结论*矛盾. ,则
,则 或
或 .易知
.易知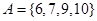 和
和 都不是
都不是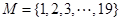 的4元基底,矛盾.
的4元基底,矛盾. 时,有
时,有 ,这时
,这时 ,
, ,易知
,易知 不是
不是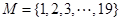 的4元基底,矛盾.
的4元基底,矛盾. 时,有
时,有 ,这时
,这时 ,
, ,易知
,易知 不是
不是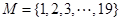 的4元基底,矛盾.
的4元基底,矛盾. 时,有
时,有 ,
, ,
, ,易知
,易知 不是
不是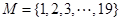 的4元基底,矛盾.
的4元基底,矛盾. 时,有
时,有 ,
, ,
, ,易知
,易知 不是
不是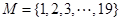 的4元基底,矛盾.
的4元基底,矛盾. 时,有
时,有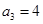 ,
, ,
, ,易知
,易知 不是
不是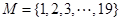 的4元基底,矛盾.
的4元基底,矛盾. 时,有
时,有 ,
, ,
,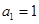 ,易知
,易知 不是
不是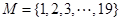 的4元基底,矛盾.
的4元基底,矛盾. 时,
时,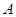 均不可能是
均不可能是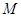 的4元基底.
的4元基底. 时,
时,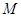 的一个基底
的一个基底 ;或{3,7,8,9,10};或{4,7,8,9,10}等,只要写出一个即可.
;或{3,7,8,9,10};或{4,7,8,9,10}等,只要写出一个即可.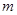 的最小可能值为5. 14分
的最小可能值为5. 14分

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com