
【题目】下列各对函数中,相同的是( )
A.f(x)=lgx2 , g(x)=2lgx
B.f(x)=lg ![]() ,g(x)=lg(x+1)﹣lg(x﹣1)
,g(x)=lg(x+1)﹣lg(x﹣1)
C.f(u)= ![]() ,g(v)=
,g(v)= ![]()
D.f(x)=x,g(x)= ![]()
科目:高中数学 来源: 题型:
【题目】如图是我国2009年至2015年生活垃圾无害化处理量(单位:亿吨)的折线图.
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2017年我国生活垃圾无害化处理量.
参考数据: ![]() yi=9.32,
yi=9.32, ![]() tiyi=40.17,
tiyi=40.17, ![]() =0.55,
=0.55, ![]() ≈2.646.
≈2.646.
参考公式:相关系数r= 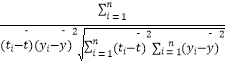 =
= 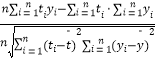
回归方程 ![]() =
= ![]() +
+ ![]() t中斜率和截距的最小二乘估计公式分别为:
t中斜率和截距的最小二乘估计公式分别为: ![]() =
= 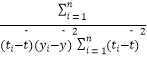 ,
, ![]() =
= ![]() ﹣
﹣ ![]() t.
t.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0),短轴长2,两焦点分别为F1 , F2 , 过F1的直线交椭圆C于M,N两点,且△F2MN的周长为8.
=1(a>b>0),短轴长2,两焦点分别为F1 , F2 , 过F1的直线交椭圆C于M,N两点,且△F2MN的周长为8.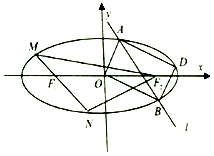
(1)求椭圆C的方程;
(2)直线l与椭圆C相交于A,B点,点D为椭圆C上一点,四边形AOBD为矩形,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月29日,中国自主研制系全球最大水陆两栖飞机AG600将于2017年5月计划首飞,AG600飞机的用途很多,最主要的是森林灭火、水上救援、物资运输、海洋探测、根据灾情监测情报部门监测得知某个时间段全国有10起灾情,其中森林灭火2起,水上救援3起,物资运输5起,现从10起灾情中任意选取3起.
(1)求三种类型灾情中各取到1个的概率;
(2)设![]() 表示取到的森林灭火的数目,求
表示取到的森林灭火的数目,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x﹣ ![]() ),x∈R的图象,只需将函数y=sin2x,x∈R的图象上所有的点( )
),x∈R的图象,只需将函数y=sin2x,x∈R的图象上所有的点( )
A.向左平行移动 ![]() 个单位长度
个单位长度
B.向右平行移动 ![]() 个单位长度
个单位长度
C.向左平行移动 ![]() 个单位长度
个单位长度
D.向右平行移动 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin2x+sinxcosx+cos2x,x∈R. 求:
(1)f(![]() )的值;
)的值;
(2)函数f(x)的最小值及相应x值;
(3)函数f(x)的递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】程序框图如图所示,现输入如下四个函数:f(x)= ![]() ,f(x)=x4 , f(x)=2x , f(x)=x﹣
,f(x)=x4 , f(x)=2x , f(x)=x﹣ ![]() ,则可以输出的函数是( )
,则可以输出的函数是( ) 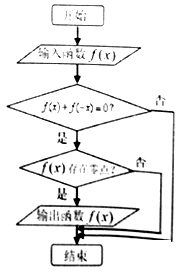
A.f(x)= ![]()
B.f(x)=x4
C.f(x)=2x
D.f(x)=x﹣ ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com