练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （18分）如图，直线与抛物线交于两点，与轴相交于点，且.

    （1）求证：点的坐标为；

    （2）求证：；

    （3）求的面积的最小值.

     

     

    【答案】

    当时，的面积取最小值1.

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

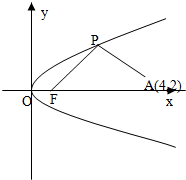    精英家教网如图所示，已知直线l的斜率为k且过点Q（-3，0），抛物线C：y2=16x，直线与抛物线l有两个不同的交点，F是抛物线的焦点，点A（4，2）为抛物线内一定点，点P为抛物线上一动点．
    （1）求|PA|+|PF|的最小值；
    （2）求k的取值范围；
    （3）若O为坐标原点，问是否存在点M，使过点M的动直线与抛物线交于B，C两点，且以BC为直径的圆恰过坐标原点，若存在，求出动点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：山东省济宁市金乡二中2011－2012学年高二下学期期中考试数学文试题 题型：044

    如图，直线与抛物线y2＝x交于A(x1，y1)，B(x2，y2)两点，与轴相交于点M，且y1y2＝－1．

    (1)求证：M点的坐标为(10)；

    (2)求证：OA⊥OB；

    (3)求△AOB的面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年西藏拉萨中学高三第5次月考数学理卷 题型：解答题

    （12分）如图，直线与抛物线，交于A,B两点，线段AB的垂直平分线与直线y+5=0交于点Q

    （1）求点Q的坐标

    （2）当点P为抛物线上位于线段AB下方（含点A,B）的动点时，求△OPQ面积的最大值

     

     

    查看答案和解析>>

    科目：高中数学 来源：2013届辽宁省高二下学期期中考试文科数学试卷（解析版） 题型：解答题

    如图，直线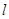与抛物线交于两点，与轴相交于点，且.

    （1）求证：点的坐标为；

    （2）求证：；

    （3）求的面积的最小值.

    【解析】设出点M的坐标，并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论，可以设其方程为,然后与抛物线方程联立消x，根据,即可建立关于的方程.求出的值.

    （2）在第（1）问的基础上，证明：即可.

    （3）先建立面积S关于m的函数关系式，根据建立即可，然后再考虑利用函数求最值的方法求最值.

     

    查看答案和解析>>

    同步练习册答案