
【题目】已知![]() ,令
,令![]() 求
求![]() 能取到的不同的整数值的个数.
能取到的不同的整数值的个数.
【答案】1005
【解析】
因为![]() ,
,![]() ,
,![]()
所以,![]() .
.
设和式![]() 中有
中有![]() 个
个![]() ,
,![]() 个
个![]() ,
,![]() 个1.则
个1.则![]() ,且
,且![]() .
.
故![]()
![]()
![]() .
.
若![]() 为整数,则
为整数,则![]() .此时,
.此时,
![]() .
.
(1)当![]() 时,
时,![]() 中至少有1007个
中至少有1007个![]() ,1007个
,1007个![]() ,即至少有2014个数,矛盾.
,即至少有2014个数,矛盾.
当![]() 时,
时,![]() 中至少有1006个
中至少有1006个![]() ,1006个
,1006个![]() .
.
(i)![]() 中有1006个
中有1006个![]() ,1007个
,1007个![]() .
.
由于![]() 中有1005个
中有1005个![]() ,则这1006个
,则这1006个![]() 在
在![]() 中连在一起,
中连在一起,
即![]() ,
,
![]() ,
,
![]() ,
,
其中,![]() .故
.故![]()
![]()
![]() .
.
(ii)![]() 中有1007个
中有1007个![]() ,1006个
,1006个![]() .类似有,
.类似有,
![]() ,
,
![]() ,
,
![]() ,
,
其中,![]() .
.
综合(i)、(ii),共有2012个![]() ,使
,使![]() 取最大值6032.
取最大值6032.
(2)用数学归纳法证明:当![]() 时,存在
时,存在![]() 使得
使得![]() .
.
当![]() 时,由(1)已证.
时,由(1)已证.
假设当![]() 时,存在
时,存在![]() 使得
使得![]() .
.
将![]() 中连续的压
中连续的压![]() (或
(或![]() )称为一段.分别从段长度大于1的
)称为一段.分别从段长度大于1的![]() 段、
段、![]() 段中各取一个,放在数列末尾(若原末尾为
段中各取一个,放在数列末尾(若原末尾为![]() ,则取出的
,则取出的![]() 放最末尾;若原末尾为
放最末尾;若原末尾为![]() ,则取出的
,则取出的![]() 放最末尾).
放最末尾).
于是,和式中的![]() 、
、![]() 各减少l,
各减少l,![]() 增加2.此时,
增加2.此时,![]() .
.
故当![]() 时,结论成立.
时,结论成立.
综上,![]() 能取到的不同整数值个数为1005.
能取到的不同整数值个数为1005.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】在一次数学会议上,任意两位数学家要么是朋友,要么是陌生人.在进餐期间,每位数学家在两个大餐厅中的其中一个就餐,每位数学家所在的餐厅中包含偶数个他(或她)的朋友.证明:数学家能被分到两个餐厅中的不同分法的数目是2的正整数次幕(即形如![]() ,其中,
,其中,![]() 是某个正整数).
是某个正整数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对一堆100粒的石子进行如下操作:每次任选石子数大于1的一堆任意分成不空的两堆,直到每堆1粒(100堆)为止.证明:
(1)无论如何操作,必有某个时刻存在20堆,其石子总数为60;
(2)可以进行适当地操作使得任何时刻不存在19堆,其石子总数为60.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)点![]() 是该抛物线上任一点,求证:过点
是该抛物线上任一点,求证:过点![]() 的抛物线的切线方程为
的抛物线的切线方程为![]() ;
;
(2)过点![]() 作该抛物线的两条切线,切点分别为
作该抛物线的两条切线,切点分别为![]() ,
,![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为 (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,动点P(x,y)到两条坐标轴的距离之和等于它到点(1,1)的距离,记点P的轨迹为曲线W,给出下列四个结论:
①曲线W关于原点对称;
②曲线W关于直线y=x对称;
③曲线W与x轴非负半轴,y轴非负半轴围成的封闭图形的面积小于![]() ;
;
④曲线W上的点到原点距离的最小值为![]()
其中,所有正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4位同学在同一天的上午、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学测试两个项目,分别在上午和下午,且每人上午和下午测试的项目不能相同.若上午不测“握力”,下午不测“台阶”,其余项目上午、下午都各测试一人,则不同的安排方式的种数为( )
A.264B.72C.266D.274
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次不等式ax2+x+b>0的解集为(-∞,-2)∪(1,+∞).
(Ⅰ)求a和b的值;
(Ⅱ)求不等式ax2-(c+b)x+bc<0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第18届国际篮联篮球世界杯(世界男子篮球锦标赛更名为篮球世界杯后的第二届世界杯)于2019年8月31日至9月15日在中国的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.中国队12名球员在第一场和第二场得分的茎叶图如图所示,则下列说法错误的是( )
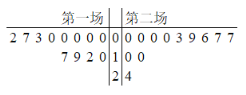
A.第一场得分的中位数为![]() B.第二场得分的平均数为
B.第二场得分的平均数为![]()
C.第一场得分的极差大于第二场得分的极差D.第一场与第二场得分的众数相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com