
【题目】已知数列![]() 、
、![]() 满足:
满足:![]() .
.
(1)求![]() ;
;
(2)设![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)设![]() ,不等式
,不等式![]() 恒成立时,求实数
恒成立时,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)由已知,整理可得递推公式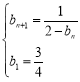 ,从而可算出
,从而可算出![]() ,
,![]() ,
,![]() ;(2)由(1)递推公式整理可得
;(2)由(1)递推公式整理可得![]() ,即
,即![]() ,且
,且![]() ,所以数列
,所以数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列,所以
为公差的等差数列,所以![]() ;(3)由(1)、(2)可求得
;(3)由(1)、(2)可求得![]() ,而
,而![]() ,
,
所以![]() ,则
,则![]() ,由条件可知
,由条件可知![]() 恒成立即可满足条件,从而构造函数
恒成立即可满足条件,从而构造函数![]() ,通过函数
,通过函数![]() 的性质可得解当
的性质可得解当![]() 时,
时,![]() 恒成立.
恒成立.
试题解析:(1)![]() ,
,
∵![]() ,∴
,∴![]() .……………………………………6分
.……………………………………6分
(2)∵![]() ,∴
,∴![]() ,
,
∴数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列.
为公差的等差数列.
∴![]() .…………………………6分
.…………………………6分
(3)由于![]() ,所以
,所以![]() ,从而
,从而![]() ,则
,则![]() .
.
![]() ,
,
∴![]() ,
,
由条件可知![]() 恒成立即可满足条件,
恒成立即可满足条件,
设![]() ,
,
当![]() 时,
时,![]() 恒成立;
恒成立;
当![]() 时,由二次函数的性质知不可能成立;
时,由二次函数的性质知不可能成立;
当![]() 时,对称轴
时,对称轴![]() ,
,![]() 在
在![]() 为单调递减函数,
为单调递减函数,
![]() ,
,
∴![]() ,∴
,∴![]() 时,
时,![]() 恒成立.
恒成立.
综上知:![]() 时,
时,![]() 恒成立.…………………………………………12分
恒成立.…………………………………………12分


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】从数列![]() 中抽出一项,依原来的顺序组成的新叫数列
中抽出一项,依原来的顺序组成的新叫数列![]() 的一个子列.
的一个子列.
(1)写出数列![]() 的一个是等比数列的子列;
的一个是等比数列的子列;
(2)若![]() 是无穷等比数列,首项
是无穷等比数列,首项![]() ,公比
,公比![]() 且
且![]() ,则数列
,则数列![]() 是否存在一个子列,为无穷等差数列?若存在,写出该子列的通项公式;若不存在,证明你的结论.
是否存在一个子列,为无穷等差数列?若存在,写出该子列的通项公式;若不存在,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() :实数
:实数![]() 满足不等式
满足不等式![]() ,
,![]() :函数
:函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)已知. “![]() ”为真命题,并记为
”为真命题,并记为![]() ,且
,且![]() :
:![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查表明,高三学生的幸福感与成绩,作业量,人际关系的满意度的指标有极强的相关性,现将这三项的满意度指标分别记为![]() ,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意.再用综合指标
,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意.再用综合指标![]() 的值评定高三学生的幸福感等级:若
的值评定高三学生的幸福感等级:若![]() ,则幸福感为一级;若
,则幸福感为一级;若![]() ,则幸福感为二级;若
,则幸福感为二级;若![]() ,则幸福感为三级. 为了了解目前某高三学生群体的幸福感情况,研究人员随机采访了该群体的10名高三学生,得到如下结果:
,则幸福感为三级. 为了了解目前某高三学生群体的幸福感情况,研究人员随机采访了该群体的10名高三学生,得到如下结果:
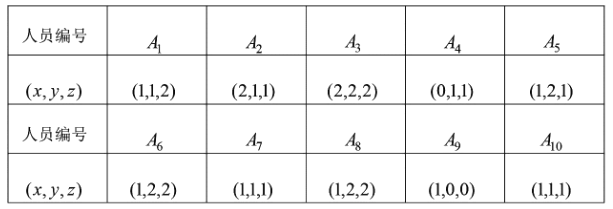
(1)在这10名被采访者中任取两人,求这两人的成绩满意度指标![]() 相同的概率;
相同的概率;
(2)从幸福感等级是一级的被采访者中任取一人,其综合指标为![]() ,从幸福感等级不是一级的被采访者中任取一人,其综合指标为
,从幸福感等级不是一级的被采访者中任取一人,其综合指标为![]() ,记随机变量
,记随机变量![]() ,求
,求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段![]() ,
, ![]() …
…![]() 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
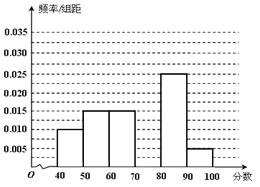
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了促进学生的全面发展,郑州市某中学重视学生社团文化建设,现用分层抽样的方法从“话剧社”,“创客社”、“演讲社”三个金牌社团中抽6人组成社团管理小组,有关数据见下表(单位:人):
社团名称 | 成员人数 | 抽取人数 |
话剧社 | 50 | a |
创客社 | 150 | b |
演讲社 | 100 | c |
(1)求![]() 的值;
的值;
(2)若从“话剧社”,“创客社”,“演讲社”已抽取的6人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com