
【题目】已知函数f(x)的图象与函数h(x)=x+![]() +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求函数f(x)的解析式;
(2)若g(x)=f(x)+![]() ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知定直线l:y=x+3,定点A(2,1),以坐标轴为对称轴的椭圆C过点A且与l相切. 
(Ⅰ)求椭圆的标准方程;
(Ⅱ)椭圆的弦AP,AQ的中点分别为M,N,若MN平行于l,则OM,ON斜率之和是否为定值?若是定值,请求出该定值;若不是定值请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,并且b=2
(1)若角A,B,C成等差数列,求△ABC外接圆的半径;
(2)若三边a,b,c成等差数列,求△ABC内切圆半径的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 若Sm﹣1=﹣4,Sm=0,Sm+2=14(m≥2,且m∈N*).
(1)求m的值;
(2)若数列{bn}满足 ![]() =logabn(n∈N*),求数列{(an+6)bn}的前n项和.
=logabn(n∈N*),求数列{(an+6)bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)已知函数![]() .
.
(Ⅰ)若函数![]() 在其定义域上是增函数,求实数
在其定义域上是增函数,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 时,求出
时,求出![]() 的极值;
的极值;
(Ⅲ)在(Ⅰ)的条件下,若![]() 在
在![]() 内恒成立,试确定
内恒成立,试确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某店销售进价为2元/件的产品![]() ,该店产品
,该店产品![]() 每日的销售量
每日的销售量![]() (单位:千件)与销售价格
(单位:千件)与销售价格![]() (单位:元/件)满足关系式
(单位:元/件)满足关系式![]() ,其中
,其中![]() .
.
(1)若产品![]() 销售价格为4元/件,求该店每日销售产品
销售价格为4元/件,求该店每日销售产品![]() 所获得的利润;
所获得的利润;
(2)试确定产品![]() 的销售价格,使该店每日销售产品
的销售价格,使该店每日销售产品![]() 所获得的利润最大.(保留1位小数)
所获得的利润最大.(保留1位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱台ABCD﹣A1B1C1D1中,底面ABCD为平行四边形,∠BAD=120°,M为CD上的点.且∠A1AB=∠A1AD=90°,AD=A1A=2,A1B1=DM=1. 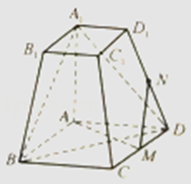
(1)求证:AM⊥A1B;
(2)若M为CD的中点,N为棱DD1上的点,且MN与平面A1BD所成角的正弦值为 ![]() ,试求DN的长.
,试求DN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆锥的轴截面SAB是边长为2的等边三角形,O为底面中心,M为SO的中点,动点P在圆锥底面内(包括圆周).若AM⊥MP,则P点形成的轨迹的长度为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com