
【题目】设数列{an}是公差大于0的等差数列,Sn为数列{an}的前n项和,已知S3=9,且2a1 , a3﹣1,a4+1构成等比数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足 ![]() =2n﹣1(n∈N*),设Tn是数列{bn}的前n项和,证明:Tn<6.
=2n﹣1(n∈N*),设Tn是数列{bn}的前n项和,证明:Tn<6.
【答案】
(1)解:∵公差不为零的等差数列{an}的前3项和S3=9,得到a2=3,
且2a1,a3﹣1,a4+1构成等比数列,
∴得到未知数a2与d的方程组: 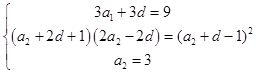 ,
,
由d≠0,解得a1=1,d=2,
∴an=2n﹣1.
(2)证明:∵数列{bn}满足 ![]() =2n﹣1(n∈N*),
=2n﹣1(n∈N*),
∴ ![]() ,∴bn=(2n﹣1)21﹣n=(4n﹣2)
,∴bn=(2n﹣1)21﹣n=(4n﹣2) ![]()
设Tn是数列{bn}的前n项和,
则Tn=2 ![]() +6
+6 ![]() +10
+10 ![]() +14
+14 ![]() +…+(4n﹣2)
+…+(4n﹣2) ![]() ,①
,①
![]() =2
=2 ![]() +6
+6 ![]() …+(4n﹣2)
…+(4n﹣2) ![]() ,②
,②
①﹣②,得: ![]() Tn=1+1+
Tn=1+1+ ![]() ﹣
﹣ ![]()
=1+ 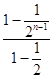 ﹣(4n﹣2)
﹣(4n﹣2) ![]() =3﹣
=3﹣ ![]() ,
,
∴Tn=6﹣ ![]() <6.
<6.
∴Tn<6.
【解析】(1)利用等差数列前n项和、通项公式和等比数列,列出方程组,求出首项与公差,由此能求出数列{an}的通项公式.(2)推导出bn=(2n﹣1)21﹣n=(4n﹣2) ![]() 利用错位相减法求出数列{bn}的前n项和,由此能证明Tn<6.
利用错位相减法求出数列{bn}的前n项和,由此能证明Tn<6.
【考点精析】关于本题考查的数列的前n项和和数列的通项公式,需要了解数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公就叫这个数列的通项公式才能得出正确答案.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公就叫这个数列的通项公式才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知a>0,b>0,c>0,函数f(x)=|x+a|﹣|x﹣b|+c的最大值为10.
(1)求a+b+c的值;
(2)求 ![]() (a﹣1)2+(b﹣2)2+(c﹣3)2的最小值,并求出此时a、b、c的值.
(a﹣1)2+(b﹣2)2+(c﹣3)2的最小值,并求出此时a、b、c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP 分成左右两部分,在PQ 左侧部分三角形POQ 为观赏区,在PQ 右侧部分种草,已知种花的单位面积的造价为3a,种草的单位面积的造价为2a,其中a 为正常数,设∠AOP=θ,种花的造价与种草的造价的和称为总造价,不计观赏区的造价,设总造价为f(θ) 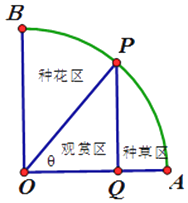
(1)求f(θ)关于θ 的函数关系式;
(2)求当θ 为何值时,总造价最小,并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知AB是半径为2的半球O的直径,P,D为球面上的两点且∠DAB=∠PAB=60°, ![]() .
. 
(1)求证:平面PAB⊥平面DAB;
(2)求二面角B﹣AP﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中,错误的是( )
A.若p为真,则¬(¬p)也为真
B.若“p∧q为真”,则“p∨q为真”为真命题
C.x∈R,使得tanx=2017
D.“2x> ![]() ”是“log
”是“log ![]() x<0”的充分不必要条件
x<0”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ2﹣4ρsinθ+2=0.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ2﹣4ρsinθ+2=0.
(Ⅰ)把圆C的极坐标方程化为直角坐标方程;
(Ⅱ)将直线l向右平移h个单位,所得直线l′与圆C相切,求h.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在以点C为圆心,且与直线BD相切的圆内运动,设 ![]() (α,β∈R),则α+β的取值范围是 .
(α,β∈R),则α+β的取值范围是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,设边a,b,c所对的角分别为A,B,C,且a>c.已知△ABC的面积为 ![]() ,
, ![]() ,b=3.
,b=3.
(Ⅰ)求a,c的值;
(Ⅱ)求sin(B﹣C)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
设函数f(x)=|x+ ![]() |+|x﹣2m|(m>0).
|+|x﹣2m|(m>0).
(Ⅰ)求证:f(x)≥8恒成立;
(Ⅱ)求使得不等式f(1)>10成立的实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com