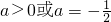已知函数f(x)=2x+a的反函数是y=f-1(x).设P(x+a,y1),Q(x,y2),R(2+a,y3)是y=f-1(x)图象上不同的三点.
(1)如果存在正实数x,使y1、y2、y3成等差数列,试用x表示实数a;
(2)在(1)的条件下,如果实数x是唯一的,试求实数a的取值范围.
解:(1)f
-1(x)=log
2(x-a),(x>a),y
1=log
2a,y
2=log
2(x-a),
y
3=log
22=1由题意,2log
2(x-a)=log
2x+1
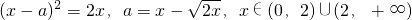
(2)由题意:关于x的方程(x-a)
2=2x即x
2-2(a+1)x+a
2=0在(a,+∞)上有唯一解.
1
0,当判别式△=0时,
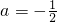
,这时方程有唯一解
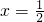
满足条件;
2
0,当判别式△>0时,方程的一个根大于a,
另一根小于a(不可能出现一根等于a的情形),
记g(x)=x
2-2(a+1)x+a
2,只需g(a)<0即可,得a>0.
解得:
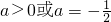
分析:(1)从原函数式中反解出x,后再进行x,y互换,即得反函数的解析式:f
-1(x)=log
2(x-a),(x>a),分别写了y
1,y
2,y
3,由题意y
1、y
2、y
3成等差数列即可表示出a;
(2)由题意:关于x的方程(x-a)
2=2x即x
2-2(a+1)x+a
2=0在(a,+∞)上有唯一解.下面对根的判别式进行分类讨论:1
0,当判别式△=0时,2
0,当判别式△>0时,利用二次函数的图象与性质即可求出实数a的取值范围.
点评:本小题主要考查反函数、等差数列的性质、一元二次方程的根的分布与系数的关系、不等式的解法等基础知识,考查运算求解能力与转化思想.属于基础题.

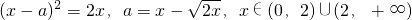
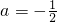 ,这时方程有唯一解
,这时方程有唯一解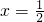 满足条件;
满足条件;