
 的距离比到定点(
的距离比到定点( ,0)的距离多1,
,0)的距离多1, 的距离比到定点(
的距离比到定点( ,0)的距离多1,得到点M与定点(
,0)的距离多1,得到点M与定点(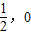 )的距离等于它到直线x=-
)的距离等于它到直线x=- 的距离,然后直接由抛物线的定义得方程;
的距离,然后直接由抛物线的定义得方程;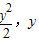 ),由两点间的距离公式写出|PA|2,换元后利用二次函数对称轴的位置讨论得到曲线C上点P到点A距离的最小值d(a).
),由两点间的距离公式写出|PA|2,换元后利用二次函数对称轴的位置讨论得到曲线C上点P到点A距离的最小值d(a). )的距离等于它到直线x=-
)的距离等于它到直线x=- 的距离.
的距离.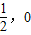 )为焦点的抛物线.
)为焦点的抛物线. ,所以p=1.即点M的轨迹方程为y2=2x;
,所以p=1.即点M的轨迹方程为y2=2x;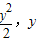 ),y∈R.则
),y∈R.则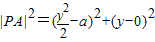 ,整理得:
,整理得: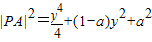 .
.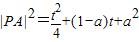 ,(t≥0)
,(t≥0)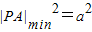 ,d(a)=|a|;
,d(a)=|a|;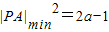 ,d(a)=
,d(a)=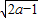 .
.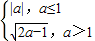 .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 3 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 2 |
| 2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com