练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．I5．函数f（x）在区间（2.5755，2.5769）上有一个零点，现研究这个零点的近似值；
    （1）如果耍精确到0.01，那么这个近似解为2.58；
    （2）如果f（2.5755）＞0，f（2.5769）＜0，f（2.5762）＞0，并给定精确度0.001，那么这个近似解为2.576．

    分析 由f（2.5755）＞0，f（2.5769）＜0，f（2.5762）＞0，结合精确度，即可得出结论．

    解答 解：（1）函数f（x）在区间（2.5755，2.5769）上有一个零点，精确到0.01，那么这个近似解为2.58，
    （2）如果f（2.5755）＞0，f（2.5769）＜0，f（2.5762）＞0，所以f（x）在区间（（2.5762，2.5769）上有一个零点，
    并给定精确度0.001，那么这个近似解为2.576，
    故答案为：（1）2.58，（2）2.276．

    点评 此题考查的是二分法求方程的近似解的问题．在解答的过程当中充分体现了同学们的运算能力以及对二分法法的应用．值得同学们体会反思．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．两平行线3x-4y-12=0与6x+ay+16=0间的距离是（　　）
    A．$\frac{28}{5}$B．4C．$\frac{14}{5}$D．$\frac{4}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

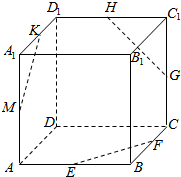    4．已知正方体ABCD-A1B1C1D1中，点E，F，G，H，K，M分别棱AB，BC，CC1，C1D1，A1D1，A1A的中点，如图，求证：EF，GH，KM共面．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知x＞1，求y=2x+$\frac{8}{x-1}$-3的最小值及此时x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．在长方体ABCD-A1B1C1D1中，AB=6，BC=4，AA1=2，P，Q分别为棱AA1，C1D1的中点，则从点P出发，沿长方体表面到达点Q的最短路径的长度为（　　）
    A．3$\sqrt{2}$B．4$\sqrt{2}$C．$\sqrt{34}$D．5$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=$\left\{\begin{array}{l}{{-x}^{2}+ax（x≤1）}\\{{a}^{2}x-7a+14（x＞1）}\end{array}\right.$，若存在x1，x2∈R，且x1≠x2，使得f（x1）=f（x2）．
    （I）求实数a的取值集合A；
    （Ⅱ）若a∈A，且函数g（x）=1g[ax2+（a+3）x+4]的值域为R，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知$\overrightarrow{OM}$=（1-$\frac{1}{3}$）$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$，则$\overrightarrow{AM}$=$\frac{1}{3}$$\overrightarrow{AB}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知非空集合S={x|-$\frac{1}{2}$≤x≤m}满足：当x∈S时，有x2∈S，则实数m的取值范围是$\frac{1}{4}$≤m≤1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=3•2x+$\frac{3}{{2}^{x}}$，x∈R．
    （1）判断函数f（x）的奇偶性，并说明理由；
    （2）利用函数单调性定义证明：f（x）在（0，+∞）上是增函数；
    （3）若f（x）≥k+log2$\frac{8}{m}$•log2（2m）（m＞0，k∈R）对任意的x∈R，任意的m∈（0，+∞）恒成立，求实数k的取值范围．

    查看答案和解析>>

    同步练习册答案