
| OP |
| OQ |
| OP |
| OQ |


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
| A、1 | B、3 | C、5 | D、4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:| xi(月) | 1 | 2 | 3 | 4 | 5 |
| yi(千克) | 0.5 | 0.9 | 1.7 | 2.1 | 2.8 |
| ? |
| y |
 |
| b |
| ? |
| a |
 |
| b |
| |||||||
|
| ? |
| a |
. |
| y |
 |
| b |
. |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| a |
| 2 |
| 4 |
| 5 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
2-x2-1-
|
| 1 |
| 3 |
| loga(-x2-x) |
查看答案和解析>>
科目:高中数学 来源: 题型:
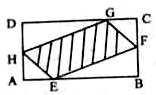 廊坊市某所中学有一块矩形空地,学校要在这块空地上修建一个内接四边形的花坛(如图所示),该花坛的四个顶点分别落在矩形的四条边上,已知 A B=a(a>2),BC=2,且 A E=A H=CF=CG,设 A E=x,花坛面积为y.
廊坊市某所中学有一块矩形空地,学校要在这块空地上修建一个内接四边形的花坛(如图所示),该花坛的四个顶点分别落在矩形的四条边上,已知 A B=a(a>2),BC=2,且 A E=A H=CF=CG,设 A E=x,花坛面积为y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com