练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知向量 =（cos ，sin ）， =（cos ，﹣sin ），且x∈[ ，π]．
    （1）求 及| + |；
    （2）求函数f（x）= +| + |的最大值，并求使函数取得最大值时x的值．

    【答案】
    （1）解： =cos cos ﹣sin sin =cos2x，

    = =1．

    | + |= = =2|cosx|，

    ∵x∈[ ，π]，∴cosx≤0．

    ∴ ═2cosx


    （2）解：由（1）可得：函数f（x）= +| + |

    =cos2x﹣2cosx

    =2cos2x﹣2cosx﹣1

    = ﹣ ，

    当x=π，cosx=﹣1时，f（x）取得最大值3


    【解析】（1）利用数量积的坐标运算、两角和差的余弦公式可得 =cos2x，由 = =1．可得| + |= ．（2）由（1）可得：函数f（x）= +| + |=cos2x﹣2cosx= ﹣ ，利用二次函数、余弦函数的单调性即可得出．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图所示，已知点A（1，0），D（﹣1，0），点B，C在单位圆O上，且∠BOC= ．
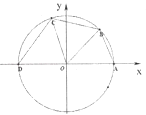
    （Ⅰ）若点B（ ， ），求cos∠AOC的值；
    （Ⅱ）设∠AOB=x（0＜x＜ ），四边形ABCD的周长为y，将y表示成x的函数，并求出y的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2+（m+2）x+（2m+5）（m≠0）的两个零点分别在区间（﹣1，0）和区间（1，2）内，则实数m的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}是等差数列，若a9+3a11＜0，a10a11＜0，且数列{an}的前n项和Sn有最大值，那么Sn取得最小正值时n等于（ ）
    A.20
    B.17
    C.19
    D.21

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知， ， ．

    （1）讨论函数的单调性；

    （2）记，设， 为函数图象上的两点，且．

    （ⅰ）当， 时，若在处的切线相互垂直，求证： ；

    （ⅱ）若在点处的切线重合，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知直线的参数方程为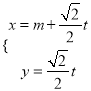（为参数），以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为，且曲线的左焦点在直线上．

    （1）若直线与曲线交于两点，求的值；

    （2）设曲线的内接矩形的周长为，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知递增等比数列{an}的第三项、第五项、第七项的积为512，且这三项 分别减去1，3，9后成等差数列．
    （1）求{an}的首项和公比；
    （2）设Sn=a12+a22+…+an2 ， 求Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用an表示自然数n的所有因数中最大的那个奇数，例如：9的因数有1，3，9，则a9=9；10的因数有1，2，5，10，则a10=5，记数列{an}的前n项和为Sn ， 则S = ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知方程C：x2+y2﹣2x﹣4y+m=0，
    （1）若方程C表示圆，求实数m的范围；
    （2）在方程表示圆时，该圆与直线l：x+2y﹣4=0相交于M、N两点，且|MN|= ，求m的值．

    查看答案和解析>>

    同步练习册答案