
【题目】设函数f(x)=x|x﹣a|,若对于任意的x1 , x2∈[﹣2,+∞),x1≠x2 , 不等式 ![]() >0恒成立,则实数a的取值范围是 .
>0恒成立,则实数a的取值范围是 .
【答案】(﹣∞,﹣4]∪{0}
【解析】解:由题意知,对于任意的x1 , x2∈[﹣2,+∞),x1≠x2 ,
不等式 ![]() >0恒成立,
>0恒成立,
∴f(x)=x|x﹣a|在[﹣2,+∞)上单调递增.
(1)当a≤﹣2时,
若x∈[﹣2,+∞),则f(x)=x(x﹣a)=x2﹣ax,其对称轴为x= ![]() ,
,
此时 ![]() ≤﹣2,所以f(x)在[﹣2,+∞)上是递增的;
≤﹣2,所以f(x)在[﹣2,+∞)上是递增的;
即a≤﹣4时满足题意;
(2)当a>﹣2且a≠0时,
①若x∈[a,+∞),则f(x)=x(x﹣a)=x2﹣ax,其对称轴为x= ![]() ,所以f(x)在[a,+∞)上是递增的;
,所以f(x)在[a,+∞)上是递增的;
②若x∈[﹣2,a),则f(x)=x(a﹣x)=﹣x2+ax,其对称轴为x= ![]() ,所以f(x)在[
,所以f(x)在[ ![]() ,a)上是递减的,
,a)上是递减的,
因此f(x)在[﹣2,a)上必有递减区间.
故可知当a>﹣2且a≠0时不成立,故舍去;
(3)当a=0时,可知函数为f(x)=x|x|= ![]() ,
,
由二次函数的性质可知,符合题意单调递增的要求,故成立
综上,实数a的取值范围是(﹣∞,﹣4]∪{0}.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() ,
, ![]() ,
, ![]() ,
, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
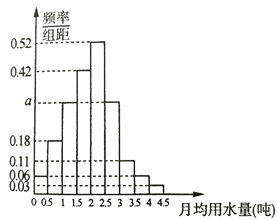
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)若将频率视为概率,从该城市居民中随机抽取3人,记这3人中月均用水量不低于3吨的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值(精确到0.01),并说明理由.
的值(精确到0.01),并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检验学习情况,某培训机构于近期举办一场竞赛活动,分别从甲、乙两班各抽取10名学员的成绩进行统计分析,其成绩的茎叶图如图所示(单位:分),假设成绩不低于90分者命名为“优秀学员”.
(1)分别求甲、乙两班学员成绩的平均分(结果保留一位小数);
(2)从甲班4名优秀学员中抽取两人,从乙班2名80分以下的学员中抽取一人,求三人平均分不低于90分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax﹣1,(a为实数),g(x)=lnx﹣x
(1)讨论函数f(x)的单调区间;
(2)求函数g(x)的极值;
(3)求证:lnx<x<ex(x>0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=cos(x+ ![]() )图象上所有点的横坐标缩短为原来的
)图象上所有点的横坐标缩短为原来的 ![]() 倍,纵坐标不变,得到函数g(x)的图象,则函数g(x)的一个减区间是( )
倍,纵坐标不变,得到函数g(x)的图象,则函数g(x)的一个减区间是( )
A.[﹣ ![]() ,
, ![]() ]
]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列![]() ,记
,记![]() ,若数列
,若数列![]() 满足:“存在
满足:“存在![]() ,使得只要
,使得只要![]() (
(![]() 且
且![]() ),必有
),必有![]() ”,则称数列
”,则称数列![]() 具有性质
具有性质![]() .
.
(Ⅰ)若数列![]() 满足
满足![]() 判断数列
判断数列![]() 是否具有性质
是否具有性质![]() ?是否具有性质
?是否具有性质![]() ?
?
(Ⅱ)求证:“![]() 是有限集”是“数列
是有限集”是“数列![]() 具有性质
具有性质![]() ”的必要不充分条件;
”的必要不充分条件;
(Ⅲ)已知![]() 是各项为正整数的数列,且
是各项为正整数的数列,且![]() 既具有性质
既具有性质![]() ,又具有性质
,又具有性质![]() ,求证:存在整数
,求证:存在整数![]() ,使得
,使得![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆C: ![]() +
+ ![]() =1(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为
=1(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为 ![]() ,且经过点(0,1).
,且经过点(0,1).
(1)求实数a,b的值;
(2)若过点P(0,m)(m>0)的直线l与椭圆C有且只有一个公共点,且l被椭圆C的伴随圆C1所截得的弦长为2 ![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=2an﹣3(﹣1)n(n∈N*).
(1)若bn=a2n﹣1,求证:bn+1=4bn;
(2)求数列{an}的通项公式;
(3)若a1+2a2+3a3+…+nan>λ2n对一切正整数n恒成立,求实数λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com