练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】四棱锥中，底面为菱形， , 为等边三角形

    （1）求证： ;

    （2）若，求二面角的余弦值.

    【答案】（1）见解析(2)0

    【解析】试题分析：（1）取中点，连结， ，由已知可得， ，又，即可证平面，从而可得；（2）求出和的值，可推出，即可证，然后建立以， ， 为， ， 轴建立空间直角坐标系，分别求出平面和的法向量，根据二面角与其法向量夹角的关系，即可得答案.

    试题解析：（1）证明：取中点，连结，

    ∵为菱形，

    ∴为等边三角形

    ∴

    ∵为等边三角形

    ∴

    ∵

    ∴

    ∵

    ∴

    (2) ∵为等边三角形，边长为2

    ∴

    ∵

    ∴

    ∴

    ∵

    ∴

    如图，以， ， 为， ， 轴建立空间直角坐标系

    则

    设平面的法向量为，则,

    取，则

    设平面的法向量为

    ,

    取，则设二面角的平面角为

    ∴，则二面角的余弦值等于0

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数 .

    （1）在区间上的极小值等于，求a的值；

    （2）令，设是函数的两个极值点，若，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设等差数列{an}的前n项和为Sn，已知(a4－1)3＋2 016(a4－1)＝1，(a2 013－1)3＋2 016·(a2 013－1)＝－1，则下列结论正确的是(　　)

    A. S2 016＝－2 016，a2 013>a4

    B. S2 016＝2 016，a2 013>a4

    C. S2 016＝－2 016，a2 013<a4

    D. S2 016＝2 016，a2 013<a4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(导学号：05856317)为了调查“小学成绩”与“中学成绩”两个变量之间是否存在相关关系，某科研机构将所调查的结果统计如下表所示：

    中学成绩不优秀

    中学成绩优秀

    总计

    小学成绩优秀

    5

    20

    25

    小学成绩不优秀

    10

    5

    15

    总计

    15

    25

    40

    则下列说法正确的是(　　)

    参考数据：

    P(K2≥k0)

    0.50

    0.40

    0.25

    0.15

    0.10

    0.05

    0.025

    0.01

    0.005

    0.001

    k0

    0.46

    0.71

    1.32

    2.07

    2.71

    3.84

    5.024

    6.635

    7.879

    10.828

    A. 在犯错误的概率不超过0.1的前提下，认为“小学成绩与中学成绩无关”

    B. 在犯错误的概率不超过0.1的前提下，认为“小学成绩与中学成绩有关”

    C. 在犯错误的概率不超过0.01的前提下，认为“小学成绩与中学成绩无关”

    D. 在犯错误的概率不超过0.01的前提下，认为“小学成绩与中学成绩有关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(导学号：05856333)

    已知椭圆C： (a>b>0)的离心率为，其右焦点为F(c,0)，第一象限的点A在椭圆C上，且AF⊥x轴．

    (Ⅰ)若椭圆C过点(1，－ )，求椭圆C的标准方程；

    (Ⅱ)已知直线l：y＝x－c与椭圆C交于M，N两点，且B(4c，yB)为直线l上的点，证明：直线AM，AB，AN的斜率满足kAB＝.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列函数：①f(x)＝()x；②f(x)＝x2；③f(x)＝x3；④f(x)＝；⑤f(x)＝log2x.其中满足条件f()>(0<x1<x2)的函数的个数是(　　)

    A. 1 B. 2

    C. 3 D. 4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知p：“x0∈(－1,1)，x－x0－m＝0(m∈R)”是正确的，设实数m的取值集合为M.

    (1)求集合M；

    (2)设关于x的不等式(x－a)(x＋a－2)<0(a∈R)的解集为N，若“x∈M”是“x∈N”的充分条件，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近年来随着我国在教育利研上的投入不断加大，科学技术得到迅猛发展，国内企业的国际竞争力得到大幅提升.伴随着国内市场增速放缓，国内确实力企业纷纷进行海外布局，第二轮企业出海潮到来，如在智能手机行业，国产品牌已在赶超国外巨头，某品牌手机公司一直默默拓展海外市场，在海外共设30多个分支机构，需要国内公司外派大量70后、80后中青年员工．该企业为了解这两个年龄层员工是否愿意被外派上作的态度，按分层抽样的方式从70后利80后的员工中随机调查了100位，得到数据如下表：

    愿意被外派

    不愿意被外派

    合计

    70后

    20

    20

    40

    80后

    40

    20

    60

    合计

    60

    40

    100

    (1)根据凋查的数据，是否有的把握认为“是否愿意被外派与年龄有关”，并说明理由；

    (2)该公司参观驻海外分支机构的交流体验活动，拟安排4名参与调查的70后员工参加，70后的员工中有愿意被外派的3人和不愿意被外派的3人报名参加，现采用随机抽样方法从报名的员工中选4人，求选到愿意被外派人数不少于不愿意被外派人数的概率.

    参考数据：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    （参考公式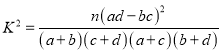： ，其中）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆，直线经过的右顶点和上顶点.

    （1）求椭圆的方程；

    （2）设椭圆的右焦点为，过点作斜率不为的直线交椭圆于两点，求的面积的最大值.

    查看答案和解析>>

    同步练习册答案