
分析 (1)由题意知,本题是一个古典概型,6根竹竿的长度从小到大依次为3.6,3.8,4.0,4.1,4.3,4.5,满足条件的事件是其中长度之差不超过0.5米的两根竹竿,先做出它的对立事件的概率,用1减去得到结果.
(2)由题意知任取两根竹竿的价格之和为ξ,则ξ的可能取值为2a,a+10,20.结合变量对应的事件写出分布列和期望,根据期望这两根竹竿的价格之和为18元,列出关于a的方程,解方程即可.
解答 解:(1)由题意知,本题是一个古典概型,
∵6根竹竿的长度从小到大依次为3.6,3.8,4.0,4.1,4.3,4.5,
其中长度之差超过0.5米的两根竹竿长可能是3.6和4.3,3.6和4.5,3.8和4.5.
设“抽取两根竹竿的长度之差不超过0.5米”为事件A,
则P($\overline{A}$)=$\frac{3}{{C}_{6}^{2}}$=$\frac{3}{15}$=$\frac{1}{5}$,
∴P(A)=1-P($\overline{A}$)=1-$\frac{1}{5}$=$\frac{4}{5}$.
∴所求的概率为$\frac{4}{5}$.
(2)设任取两根竹竿的价格之和为ξ,则ξ的可能取值为2a,a+10,20.
其中P(ξ=2a)=$\frac{1}{{C}_{6}^{2}}$=$\frac{1}{15}$,
P(ξ=a+10)=$\frac{{C}_{2}^{1}{C}_{4}^{1}}{{C}_{6}^{2}}$=$\frac{8}{15}$,
P(ξ=20)=$\frac{{C}_{4}^{2}}{{C}_{6}^{2}}$=$\frac{6}{15}$.
∴Eξ=2a×$\frac{1}{15}$+(a+10)×$\frac{8}{15}$+20×$\frac{6}{15}$=$\frac{2a+40}{3}$=18,
∴a=7
点评 本题考查古典概型,考查对立事件的概率,考查离散型随机变量的分布列和期望,考查的不是求期望,而是利用期望的值求式子中出现的一个变量,利用解方程的思想.


科目:高中数学 来源: 题型:解答题
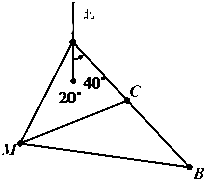 如图,已知点M在A城的南偏西20°的方向上,现有一辆汽车在点B沿公路向A城行驶,公路的走向是A城的南偏东40°.开始时,汽车到M的距离为31km,汽车前进20km到达点C时,到M的距离缩短了10km,问汽车还要行驶多远才能到达A城?
如图,已知点M在A城的南偏西20°的方向上,现有一辆汽车在点B沿公路向A城行驶,公路的走向是A城的南偏东40°.开始时,汽车到M的距离为31km,汽车前进20km到达点C时,到M的距离缩短了10km,问汽车还要行驶多远才能到达A城?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
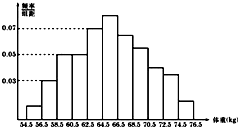 为了了解某市高三学生的身体发育情况,抽测了该市50名高三男生的体重(kg),数据得到的频率分布直方图如图.根据右图可知这50名男生中体重在[56.5,60.5]的人数是8.
为了了解某市高三学生的身体发育情况,抽测了该市50名高三男生的体重(kg),数据得到的频率分布直方图如图.根据右图可知这50名男生中体重在[56.5,60.5]的人数是8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,1) | B. | (1,2) | C. | (-1,-2) | D. | (2,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
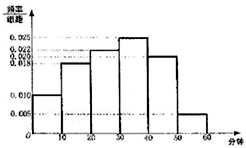 电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图;
电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图; | 非体育迷 | 体育迷 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com