
【题目】公车私用、超编配车等现象一直饱受诟病,省机关事务管理局认真贯彻落实党中央、国务院有关公务用车配备使用管理办法,积极推进公务用车制度改革.某机关单位有车牌尾号为2的汽车A和尾号为6的汽车B,两车分属于两个独立业务部门.为配合用车制度对一段时间内两辆汽车的用车记录进行统计,在非限行日,A车日出车频率0.6,B车日出车频率0.5,该地区汽车限行规定如下:
车尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
现将汽车日出车频率理解为日出车概率,且A,B两车出车情况相互独立.
(1)求该单位在星期一恰好出车一台的概率;
(2)设X表示该单位在星期一与星期二两天的出车台数之和,求X的分布列及其数学期望E(X).
【答案】
(1)解:设A车在星期出车的事件为Ai,B车在星期出车的事件为Bi,i=1,2,3,4,5.
由已知可得P(Ai)=0.6,P(Bi)=0.5,
设该单位在星期一恰好出一台车的事件为C,
因为A,B两车是否出车相互独立,且事件 ![]() ,
, ![]() 互斥,
互斥,
所以P(C)=P( ![]() +
+ ![]() )=P(
)=P( ![]() )+P(
)+P( ![]() )
)
=0.6×(1﹣0.5)+(1﹣0.6)×0.5=0.5,
所以该单位在星期一恰好出一台车的概率为0.5
(2)解:X的可能取值为0,1,2,3,
P(X=0)=P( ![]() )P(
)P( ![]() )=0.4×0.5×0.4=0.08,
)=0.4×0.5×0.4=0.08,
P(X=1)=P(C)P( ![]() )+P(
)+P( ![]() )P(A2)=0.5×0.4+0.4×0.5×0.6=0.32,
)P(A2)=0.5×0.4+0.4×0.5×0.6=0.32,
P(X=2)=P(A1B1)P( ![]() P+P(C)P(A2)=0.6×0.5×0.4+0.5×0.6=0.42,
P+P(C)P(A2)=0.6×0.5×0.4+0.5×0.6=0.42,
P(X=3)=P(A1B1)P(A2)=0.6×0.5×0.6=0.18.
所以X的分布列为
X | 0 | 1 | 2 | 3 |
P | 0.08 | 0.32 | 0.42 | 0.18 |
EX=0×0.08+1×0.32+2×0.42+3×0.18=1.7
【解析】(1)设A车在星期出车的事件为Ai , B车在星期出车的事件为Bi , i=1,2,3,4,5.由已知可得P(Ai)=0.6,P(Bi)=0.5,设该单位在星期一恰好出一台车的事件为C,因为A,B两车是否出车相互独立,且事件 ![]() ,
, ![]() 互斥,由此能求出该单位在星期一恰好出一台车的概率.(2)X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列及其数学期望E(X).
互斥,由此能求出该单位在星期一恰好出一台车的概率.(2)X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列及其数学期望E(X).


科目:高中数学 来源: 题型:
【题目】综合题。
(1)若cos ![]() =
= ![]() ,
, ![]() π<x<
π<x< ![]() π,求
π,求 ![]() 的值.
的值.
(2)已知函数f(x)=2 ![]() sinxcosx+2cos2x﹣1(x∈R),若f(x0)=
sinxcosx+2cos2x﹣1(x∈R),若f(x0)= ![]() ,x0∈[
,x0∈[ ![]() ,
, ![]() ],求cos2x0的值.
],求cos2x0的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+)(其中A>0,||< ![]() ,ω>0)的图象如图所示,
,ω>0)的图象如图所示, 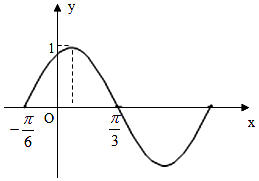
(1)求函数f(x)的解析式;
(2)若关于x的方程f(x)+ ![]() cos2x﹣
cos2x﹣ ![]() sin2x﹣k=0在[0,
sin2x﹣k=0在[0, ![]() ]上只有一解,求k的取值范围.
]上只有一解,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有0,1,2,3,4,5六个数字.
(1)用所给数字能够组成多少个四位数?
(2)用所给数字可以组成多少个没有重复数字的五位数?
(3)用所给数字可以组成多少个没有重复数字且比3142大的数?(最后结果均用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知面积为S的凸四边形中,四条边长分别记为a1 , a2 , a3 , a4 , 点P为四边形内任意一点,且点P到四边的距离分别记为h1 , h2 , h3 , h4 , 若 ![]() =
= ![]() =
= ![]() =
= ![]() =k,则h1+2h2+3h3+4h4=
=k,则h1+2h2+3h3+4h4= ![]() 类比以上性质,体积为y的三棱锥的每个面的面积分别记为Sl , S2 , S3 , S4 , 此三棱锥内任一点Q到每个面的距离分别为H1 , H2 , H3 , H4 , 若
类比以上性质,体积为y的三棱锥的每个面的面积分别记为Sl , S2 , S3 , S4 , 此三棱锥内任一点Q到每个面的距离分别为H1 , H2 , H3 , H4 , 若 ![]() =
= ![]() =
= ![]() =
= ![]() =K,则H1+2H2+3H3+4H4=( )
=K,则H1+2H2+3H3+4H4=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com