练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

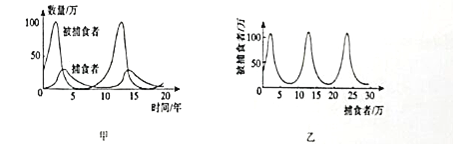
    【题目】图甲中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律、对捕食者和被捕食者数量之间的关系描述错误的是（ ）

    A. 捕食者和被捕食者数量与时间以年为周期

    B. 由图可知，当捕食者数量增多的过程中，被捕食者数量先增多后减少

    C. 捕食者和被捕食者数量之间的关系可以用图1乙描述

    D. 捕食者的数量在第年和年之间数量在急速减少

    【答案】C

    【解析】分析：由题意可知：捕食者和被捕食者数量与时间以10年为周期呈周期性变化，故捕食者和被捕食者数量之间的关系应为环状，进而得到答案

    详解：由已知中某理想状态下捕食者和被捕食者数量随时间的变化规律．

    可得捕食者和被捕食者数量与时间以10年为周期呈周期性变化，

    捕食者的数量在第25年和30年之间数量在急速减少，正确；

    由图可知，当捕食者数量增多的过程中，被捕食者数量先增多后减少，

    故捕食者和被捕食者数量之间的关系应为环状，

    捕食者和被捕食者数量之间的关系可以用图1乙描述，显然不正确；

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在正方体 中， 分别为 的中点，点 是底面内一点，且 平面 ，则 的最大值是( )

    A. B. 2 C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在菱形中，，平面，，是线段的中点，.

    （1）证明：平面；

    （2）求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若直角坐标平面内的两点P，Q满足条件：①P，Q都在函数的图像上；②P，Q关于原点对称，则称P，Q是函数的一对“友好点对”（点对P，Q与Q，P看作同一对“友好点对”）.已知函数若此函数的“友好点对”有且只有一对，则a的取值范围是（ ）

    A.B.

    C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关, 现收集了该种药用昆虫的6组观测数据如下表：

    温度x/C

    21

    23

    24

    27

    29

    32

    产卵数y/个

    6

    11

    20

    27

    57

    77

    经计算得： ， ， ， ，

    ，线性回归模型的残差平方和，e8.0605≈3167，其中xi, yi分别为观测数据中的温度和产卵数，i=1, 2, 3, 4, 5, 6.

    (Ⅰ)若用线性回归模型，求y关于x的回归方程=x+（精确到0.1）；

    (Ⅱ)若用非线性回归模型求得y关于x的回归方程为=0.06e0.2303x，且相关指数R2=0.9522.

    ( i )试与(Ⅰ)中的回归模型相比，用R2说明哪种模型的拟合效果更好.

    ( ii )用拟合效果好的模型预测温度为35C时该种药用昆虫的产卵数（结果取整数）.

    附：一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线=x+的斜率和截距的最小二乘估计为

    =；相关指数R2=．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准（吨）、一位居民的月用水量不超过的部分按平价收费，超出的部分按议价收费.为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0,0.5)，[0.5,1)，…，[4,4.5]分成9组，制成了如图所示的频率分布直方图.

    （Ⅰ）求直方图中a的值；

    （Ⅱ）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；

    （Ⅲ）若该市政府希望使85%的居民每月的用水量不超过标准（吨），估计的值，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求函数在上的最大值；

    （2）令，若在区间上为单调递增函数，求的取值范围；

    （3）当 时，函数 的图象与轴交于两点 ，且 ，又是的导函数.若正常数 满足条件.证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某大学生从全校学生中随机选取名统计他们的鞋码大小，得到如下数据：

    鞋码

    合计

    男生

    女生

    以各性别各鞋码出现的频率为概率．

    （）从该校随机挑选一名学生，求他（她）的鞋码为奇数的概率．

    （）为了解该校学生考试作弊的情况，从该校随机挑选名学生进行抽样调查．每位学生从装有除颜色外无差别的个红球和个白球的口袋中，随机摸出两个球，若同色，则如实回答其鞋码是否为奇数；若不同色，则如实回答是否曾在考试中作弊．这里的回答，是指在纸上写下“是”或“否”．若调查人员回收到张“是”的小纸条，试估计该校学生在考试中曾有作弊行为的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某网购平台为了解某市居民在该平台的消费情况，从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名，并绘制右图所示频率分布直方图，已知之间三组的人数可构成等差数列.

    （1）求的值；

    （2）分析人员对100名调查对象的性别进行统计发现，消费金额不低于300元的男性有20人，低于300元的男性有25人，根据统计数据完成下列列联表，并判断是否有的把握认为消费金额与性别有关？

    （3）分析人员对抽取对象每周的消费金额与年龄进一步分析，发现他们线性相关，得到回归方程.已知100名使用者的平均年龄为38岁，试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.（同一组数据用该区间的中点值代替）

    ，其中

    查看答案和解析>>

    同步练习册答案