
【题目】设圆![]() 的圆心在
的圆心在![]() 轴上,并且过
轴上,并且过![]() 两点.
两点.
(1)求圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,那么以
两点,那么以![]() 为直径的圆能否经过原点,若能,请求出直线
为直径的圆能否经过原点,若能,请求出直线![]() 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
【答案】(1) ![]() (2)
(2) ![]() 或
或![]() .
.
【解析】试题分析:(1)圆![]() 的圆心在
的圆心在![]() 的垂直平分线上,又
的垂直平分线上,又![]() 的中点为
的中点为![]() ,
, ![]() ,∴
,∴![]() 的中垂线为
的中垂线为![]() .∵圆
.∵圆![]() 的圆心在
的圆心在![]() 轴上,∴圆
轴上,∴圆![]() 的圆心为
的圆心为![]() ,因此,圆
,因此,圆![]() 的半径
的半径![]() ,(2)设M,N的中点为H,假如以
,(2)设M,N的中点为H,假如以![]() 为直径的圆能过原点,则
为直径的圆能过原点,则![]() .
.![]() ,设
,设![]() 是直线
是直线![]() 与圆
与圆![]() 的交点,将
的交点,将![]() 代入圆
代入圆![]() 的方程得:
的方程得: ![]() .∴
.∴![]() .∴
.∴![]() 的中点为
的中点为![]() .代入即可求得
.代入即可求得![]() ,解得
,解得![]() .再检验即可
.再检验即可
试题解析:
(1)∵圆![]() 的圆心在
的圆心在![]() 的垂直平分线上,
的垂直平分线上,
又![]() 的中点为
的中点为![]() ,
, ![]() ,∴
,∴![]() 的中垂线为
的中垂线为![]() .
.
∵圆![]() 的圆心在
的圆心在![]() 轴上,∴圆
轴上,∴圆![]() 的圆心为
的圆心为![]() ,
,
因此,圆![]() 的半径
的半径![]() ,
,
∴圆![]() 的方程为
的方程为![]() .
.
(2)设![]() 是直线
是直线![]() 与圆
与圆![]() 的交点,
的交点,
将![]() 代入圆
代入圆![]() 的方程得:
的方程得: ![]() .
.
∴![]() .
.
∴![]() 的中点为
的中点为![]() .
.
假如以![]() 为直径的圆能过原点,则
为直径的圆能过原点,则![]() .
.
∵圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
∴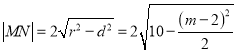 .
.
∴![]() ,解得
,解得![]() .
.
经检验![]() 时,直线
时,直线![]() 与圆
与圆![]() 均相交,
均相交,
∴![]() 的方程为
的方程为![]() 或
或![]() .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】把正整数排成如图(a)的三角形阵,然后擦去第偶数行中的所有奇数,第奇数行中的所有偶数,可得如图(b)三角形阵,现将图(b)中的正整数按从小到大的顺序构成一个数列{an},若ak=2017,则k= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信是现代生活中进行信息交流的重要工具.据统计,某公司200名员工中90%的人使用微信,其中每天使用微信时间在一小时以内的有60人,其余的员工每天使用微信时间在一小时以上,若将员工分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,那么使用微信的人中75%是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,那么经常使用微信的员工中都是青年人.
(1)若要调查该公司使用微信的员工经常使用微信与年龄的关系,列出并完成2×2列联表:

(2)由列联表中所得数据判断,是否有99.9%的把握认为“经常使用微信与年龄有关”?
(3)采用分层抽样的方法从“经常使用微信”的人中抽取6人,从这6人中任选2人,求选出的2人,均是青年人的概率.
附:

![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司购买了A,B,C三种不同品牌的电动智能送风口罩.为了解三种品牌口罩的电池性能,现采用分层抽样的方法,从三种品牌的口罩中抽出25台,测试它们一次完全充电后的连续待机时长,统计结果如下(单位:小时):
A | 4 | 4 | 4.5 | 5 | 5.5 | 6 | 6 | |||
B | 4.5 | 5 | 6 | 6.5 | 6.5 | 7 | 7 | 7.5 | ||
C | 5 | 5 | 5.5 | 6 | 6 | 7 | 7 | 7.5 | 8 | 8 |
(Ⅰ)已知该公司购买的C品牌电动智能送风口罩比B品牌多200台,求该公司购买的B品牌电动智能送风口罩的数量;
(Ⅱ)从A品牌和B品牌抽出的电动智能送风口罩中,各随机选取一台,求A品牌待机时长高于B品牌的概率;
(Ⅲ)再从A,B,C三种不同品牌的电动智能送风口罩中各随机抽取一台,它们的待机时长分别是a,b,c(单位:小时).这3个新数据与表格中的数据构成的新样本的平均数记为![]() ,表格中数据的平均数记为
,表格中数据的平均数记为![]() .若
.若![]() ,写出a+b+c的最小值(结论不要求证明).
,写出a+b+c的最小值(结论不要求证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() 与动直线
与动直线![]() 的交点为
的交点为![]() ,线段
,线段![]() 的中垂线与动直线
的中垂线与动直线![]() 的交点为
的交点为![]() .
.

(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过动点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
,![]() ,求证:
,求证:![]() 的大小为定值.
的大小为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.那么在一个生产周期内该企业生产甲、乙两种产品各多少吨可获得最大利润,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com