若函数
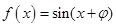
是偶函数,则
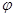
可取的一个值为( )
本题考查偶函数的判定。
点拨:三角函数中只有余弦函数是偶函数。
解答:当
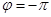
时,
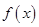
是奇函数。
当
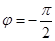
时,
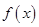
是偶函数。
当
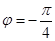
时,
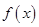
是非奇非偶函数。
当
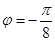
时,
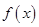
也是非奇非偶函数。
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分14分)
设函数
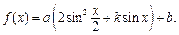
(1)当
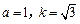
时,求函数
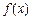
的单调减区间;
(2)当
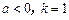
时,函数
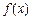
在
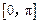
上的值域是[2,3],求a,b的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设
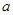
为函数
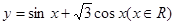
的最大值,则二项式
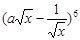
的展开式中含
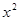
项的系数是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
已知函数
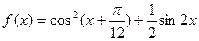
.
(1)求
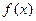
的最值;
(2)求
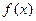
的单调增区间.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)已知角
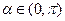
,向量
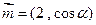
,
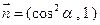
,且
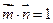
,
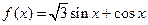
。
(Ⅰ)求角
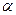
的大小;(Ⅱ)求函数
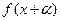
的单调递减区间。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
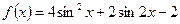
(
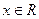
)
(1)求
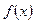
的最小正周期,
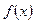
的最大值及

此时
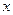
的取值集合
(2)证明函数
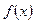
的图像关于
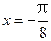
对称 (12分)
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分1

2分)
已知函数
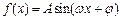
(
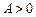
,
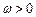
,
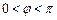

)在
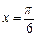
取得最大值2,方程
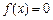
的两个根为
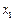
、
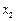
,且
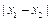
的最小值为
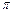
.
(Ⅰ)求
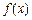
;
(Ⅱ)将函数
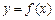
图象上各点的横坐标压缩到原来的
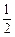
,纵坐标不变,得到函数
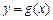
的图象.当
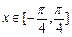
时,函数
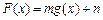
(m、n∈R)的值域是
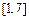
,求实数m、n的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
函数
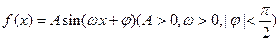
的部分图象如图所示。
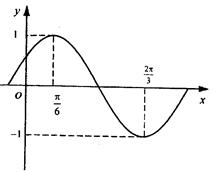
(I)求
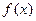
的最小正周期及解析式;
(II)设
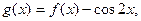
求函数
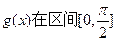
上的最大值和最小值
查看答案和解析>>

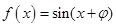 是偶函数,则
是偶函数,则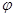 可取的一个值为( )
可取的一个值为( )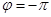
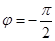
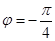
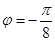
 2分)
2分)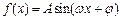 (
(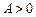 ,
,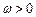 ,
,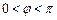
 )在
)在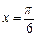 取得最大值2,方程
取得最大值2,方程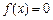 的两个根为
的两个根为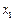 、
、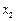 ,且
,且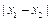 的最小值为
的最小值为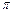 .
.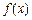 ;
;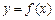 图象上各点的横坐标压缩到原来的
图象上各点的横坐标压缩到原来的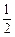 ,纵坐标不变,得到函数
,纵坐标不变,得到函数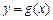 的图象.当
的图象.当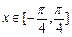 时,函数
时,函数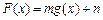 (m、n∈R)的值域是
(m、n∈R)的值域是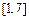 ,求实数m、n的值.
,求实数m、n的值.