
【题目】已知圆C:x2+y2﹣2x﹣1=0,直线l:3x﹣4y+12=0,圆C上任意一点P到直线l的距离小于2的概率为 .
【答案】![]()
【解析】解:由题意知圆的标准方程为(x﹣1)2+y2=2的圆心是(1,0), 圆心到直线3x﹣4y+12=0的距离是d= ![]() =
= ![]() =3,
=3,
当与3x﹣4y+12=0平行,且在直线下方距离为2的平行直线为3x﹣4y+b=0,
则d= ![]() =
= ![]() =2,则|b﹣12|=10,
=2,则|b﹣12|=10,
即b=22(舍)或b=2,此时直线为3x﹣4y+2=0,
则此时圆心到直线3x﹣4y+2=0的距离d=1,即三角形ACB为直角三角形,
当P位于弧ADB时,此时P到直线l的距离小于2,
则根据几何概型的概率公式得到P= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】本题主要考查了几何概型的相关知识点,需要掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在单位正方体ABCD﹣A1B1C1D1中,O是B1D1的中点,如图建立空间直角坐标系. 
(1)求证:B1C∥平面ODC1;
(2)求异面直线B1C与OD夹角的余弦值;
(3)求直线B1C到平面ODC1的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在直线x﹣2y=0上.
(1)若圆C与y轴的正半轴相切,且该圆截x轴所得弦的长为2 ![]() ,求圆C的标准方程;
,求圆C的标准方程;
(2)在(1)的条件下,直线l:y=﹣2x+b与圆C交于两点A,B,若以AB为直径的圆过坐标原点O,求实数b的值;
(3)已知点N(0,3),圆C的半径为3,且圆心C在第一象限,若圆C上存在点M,使MN=2MO(O为坐标原点),求圆心C的纵坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直三棱柱ABC﹣A1B1C1中,AB=AA1=2,∠ABC=90°,点E、F分别是棱AB、BB1的中点,当二面角C1﹣AA1﹣B为45o时,直线EF和BC1所成的角为( ) 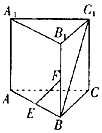
A.45o
B.60o
C.90o
D.120o
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数![]() .
.
(1)若x=2是函数f(x)的极值点,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若函数f(x)在![]() 上为单调增函数,求a的取值范围;
上为单调增函数,求a的取值范围;
(3)设m,n为正实数,且m>n,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(2,1)
(1)点A(﹣1,3)和点B(3,1)到直线l的距离相等,求直线l的方程;
(2)若直线l与x正半轴、y正半轴分别交于A,B两点,且△ABO的面积为4,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文科做)已知函数f(x)=x﹣ ![]() ﹣(a+2)lnx,其中实数a≥0.
﹣(a+2)lnx,其中实数a≥0.
(1)若a=0,求函数f(x)在x∈[1,3]上的最值;
(2)若a>0,讨论函数f(x)的单调性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com