Question

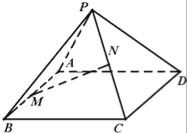
【题目】已知正四棱锥P﹣ABCD如图．

（Ⅰ）若其正视图是一个边长分别为、，2的等腰三角形，求其表面积S、体积V；

（Ⅱ）设AB中点为M，PC中点为N，证明：MN∥平面PAD．

Answer 1

【答案】（Ⅰ）（Ⅱ）详见解析

【解析】

试题分析：（I）作出棱锥的高和斜高，利用勾股定理求出棱锥的高，代入面积，体积公式计算；（II）取PD的中点Q，证明AMNQ是平行四边形得出MN∥AQ，于是MN∥平面PAD

试题解析：（I）过P作PE⊥CD于E，过P作PO⊥平面ABCD，垂足为O，

则PE⊥CD，E为CD的中点，O为正方形ABCD的中心．

∵正四棱锥的正视图是一个边长分别为、，2的等腰三角形，

∴PE=，BC=CD=2，

∴OE=，∴PO==．

∴正四棱锥的表面积S=S正方形ABCD+4S△PCD=22+4×=4+4．

正四棱锥的体积V===．

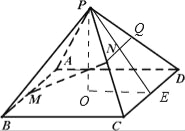
（II）过N作NQ∥CD，连结AQ，

∵N为PC的中点，∴Q为PD的中点，

∴NQCD，又AMCD，

∴AMNQ，

∴四边形AMNQ是平行四边形，

∴MN∥AQ，又MN平面PAD，AQ平面PAD，

∴MN∥平面PAD．