
【题目】对于数列![]() ,若
,若![]() (
(![]() 是与
是与![]() 无关的常数,
无关的常数,![]() )则称数列
)则称数列![]() 叫做“弱等差数列”已知数列
叫做“弱等差数列”已知数列![]() 满足:
满足:![]() 且
且![]() ,对于
,对于![]() 恒成立,(其中
恒成立,(其中![]() 都是常数)
都是常数)
(1)求证:数列![]() 是“弱等差数列”,并求出数列
是“弱等差数列”,并求出数列![]() 的通项公式
的通项公式
(2)当![]() 时,若数列
时,若数列![]() 是单调递增数列,求
是单调递增数列,求![]() 的取值范围
的取值范围
(3)若![]() ,且
,且![]() ,数列
,数列![]() 满足:
满足:![]() ,求
,求![]()
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形BCEF中,∠CBF=∠BCE=90°,A,D分别是BF,CE上的点,AD∥BC,且AB=DE=2BC=2AF(如图1),将四边形ADEF沿AD折起,连结BE、BF、CE(如图2).在折起的过程中,下列说法中正确的个数( )
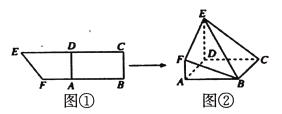
①AC∥平面BEF;
②B、C、E、F四点可能共面;
③若EF⊥CF,则平面ADEF⊥平面ABCD;
④平面BCE与平面BEF可能垂直
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() :
:![]()
![]() 的左、右焦点,且椭圆
的左、右焦点,且椭圆![]() 上的点到点
上的点到点![]() 的距离的最小值为
的距离的最小值为![]() .点M、N是椭圆
.点M、N是椭圆![]() 上位于
上位于![]() 轴上方的两点,且向量
轴上方的两点,且向量![]() 与向量
与向量![]() 平行.
平行.
(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 时,求△
时,求△![]() 的面积;
的面积;
(3)当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对于任意
,对于任意![]() 满足
满足![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,其前
,其前![]() 项和为
项和为![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:对于任意正整数
,求证:对于任意正整数![]() ,都有
,都有![]() ;
;
(3)将数列![]() 、
、![]() 的项按照“当
的项按照“当![]() 为奇数时,
为奇数时,![]() 放在前面”,“当
放在前面”,“当![]() 为偶数时,
为偶数时,![]() 放在前面”的要求进行“交叉排列”得到一个新的数列:
放在前面”的要求进行“交叉排列”得到一个新的数列:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 求这个新数列的前
求这个新数列的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(Ⅱ)设函数![]() ,在(Ⅰ)的条件下,试判断
,在(Ⅰ)的条件下,试判断![]() 在
在![]() 上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】垃圾分一分,城市美十分;垃圾分类,人人有责.某市为进一步推进生活垃圾分类工作,调动全民参与的积极性,举办了“垃圾分类游戏挑战赛”.据统计,在为期![]() 个月的活动中,共有
个月的活动中,共有![]() 万人次参与.为鼓励市民积极参与活动,市文明办随机抽取
万人次参与.为鼓励市民积极参与活动,市文明办随机抽取![]() 名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
单次游戏得分 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)根据数据,估计参与活动的网友单次游戏得分的平均值及标准差(同一组中的数据用该组区间的中点值作代表);(其中标准差的计算结果要求精确到![]() )
)
(2)若要从单次游戏得分在![]() 、
、![]() 、
、![]() 的三组参与者中,用分层抽样的方法选取
的三组参与者中,用分层抽样的方法选取![]() 人进行电话回访,再从这
人进行电话回访,再从这![]() 人中任选
人中任选![]() 人赠送话费,求此
人赠送话费,求此![]() 人单次游戏得分不在同一组内的概率.
人单次游戏得分不在同一组内的概率.
附:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为配合“2019双十二”促销活动,某公司的四个商品派送点如图环形分布,并且公司给![]() 四个派送点准备某种商品各50个.根据平台数据中心统计发现,需要将发送给
四个派送点准备某种商品各50个.根据平台数据中心统计发现,需要将发送给![]() 四个派送点的商品数调整为40,45,54,61,但调整只能在相邻派送点进行,每次调动可以调整1件商品.为完成调整,则( )
四个派送点的商品数调整为40,45,54,61,但调整只能在相邻派送点进行,每次调动可以调整1件商品.为完成调整,则( )

A.最少需要16次调动,有2种可行方案
B.最少需要15次调动,有1种可行方案
C.最少需要16次调动,有1种可行方案
D.最少需要15次调动,有2种可行方案
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com