
过点
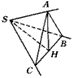
S引三条不共面的直线SA、SB、SC,如图,∠BSC=90°,∠ASC=∠ASB=60°,若截取SA=SB=SC=α.求证:平面ABC⊥平面BSC.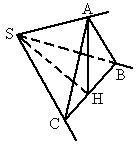
|
要证明平面 ABC上平面BSC,根据面面垂直的判定定理,需在平面ABC或平面BSC内找到一条与另一个平面垂直的直线.证法1:∵SA=SB=SC=a, ,∴△ASNB和△ASC都是等边三角形,∴AB=AC=a取BC的中点为H,连结AH,SH,∴AH⊥BC,SH⊥BC,在Rt△BSC中,BS=CS=a,∴BC= ,∴△ASNB和△ASC都是等边三角形,∴AB=AC=a取BC的中点为H,连结AH,SH,∴AH⊥BC,SH⊥BC,在Rt△BSC中,BS=CS=a,∴BC= . .
∴  , ,
 , , , , ,∴ ,∴ ,∴AH⊥SH.∴AH⊥平面SBC.∵AH ,∴AH⊥SH.∴AH⊥平面SBC.∵AH 平面ABC,∴平面ABC⊥平面SBC 平面ABC,∴平面ABC⊥平面SBC
证法 2:∵SA=AC=AB,∴顶点A在平面BSC内的射影H为△BSC的外心.又△BSC为直角三角形,∴H在斜边BC上,又△BSC为等腰直角三角形,∴H为BC的中点,∴AH⊥平面BSC.∵AH 不面ABC,∴平面ABC⊥平面BSC。 不面ABC,∴平面ABC⊥平面BSC。 |


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源:浙江省严州中学2011-2012学年高二10月阶段性测试数学理科试题 题型:047
如图,过点S引三条不共面的直线SA,SB,SC,其中∠BSC=90°,∠ASB=∠ASC=60°,且SA=SB=SC=a.
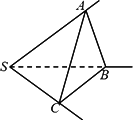
求证:平面ABC⊥平面BSC.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
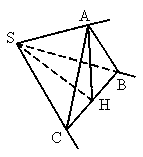
过点S引三条不共面的直线SA、SB、SC,如图,∠BSC=90°,∠ASC=∠ASB=60°,若截取SA=SB=SC=a.
(1)求证:平面ABC⊥平面BSC;
(2)求S到平面ABC的距离.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:047
过点S引三条不共面的直线SA、SB、SC,如图,∠BSC=90°,∠ASC=∠ASB=60°,若截取SA=SB=SC=α.求证:平面ABC⊥平面BSC.
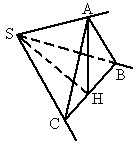
查看答案和解析>>
科目:高中数学 来源:同步题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com