练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知曲线C1:y=x2与C2:y=-(x-2)2,若直线l与C1、C2都相切,求直线l的方程.

    分析：设出直线l与C1、C2的切点坐标,可以分别用一个参数来表示,利用导数的几何意义求出切线的斜率,利用斜率相等可求出两切点的坐标.

    解法一：设直线l与两曲线的切点的坐标分别为A(a,a2),B(b,-(b-2)2).

    因为两曲线对应函数的导函数分别为y1′=2x,y2′=-2(x-2)，

    所以在A、B两点处两曲线的斜率分别为y1′|x=a=2a,y2′|x=b=-2(b-2).

    由题意,可得=2a=-2b+4,

    解得

    所以A为(2,4)或(0,0),切线的斜率k=4或0,从而得到切线l的方程为y=4x-4或y=0.

    解法二：设l与C1、C2的切点的横坐标分别为a、b,直线l的斜率为k,

    根据题意,得y1′=2x,y2′=-2(x-2).

    y1′|x=a=2a,y2′|x=b=-2(b-2).

    由k=2a=-2b+4,可得a=,b=,

    则l与C1、C2的切点的坐标分别为

    则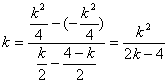,解得k=0或4.

    故所求的切线方程为y=4x-4或y=0.

    绿色通道:

    本题是导数的一个具体的应用,在解题过程中一般先设出切点的坐标,再利用方程组求出参数的取值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知曲线C1：
    |x|
    a
    +
    |y|
    b
    =1(a＞b＞0)    所围成的封闭图形的面积为4
    		5
    ，曲线C1的内切圆半径为
    2
    		5
    3
    ．记C2为以曲线C1与坐标轴的交点为顶点的椭圆．
    （Ⅰ）求椭圆C2的标准方程；
    （Ⅱ）设AB是过椭圆C2中心的任意弦，l是线段AB的垂直平分线．M是l上异于椭圆中心的点．
    （1）若|MO|=λ|OA|（O为坐标原点），当点A在椭圆C2上运动时，求点M的轨迹方程；
    （2）若M是l与椭圆C2的交点，求△AMB的面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知曲线C1：
    x=-4+cost
    y=3+sint
    （t为参数），C2：
    x=8cosθ
    y=3sinθ
    （θ为参数）．
    （Ⅰ）将C1，C2的方程化为普通方程；
    （Ⅱ）若C1上的点P对应的参数为DF=
    		MF2+DM2
    =
    		302+1702
    =10
    		198
    ，Q为C2上的动点，求PQ中点M到直线C3：x-2y-7=0距离的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•湖南）在直角坐标系xoy 中，已知曲线C1：
    x=t+1
    y=1-2t
    （t为参数）与曲线C2：
    x=asinθ
    y=3cosθ
    （θ为参数，a＞0 ）有一个公共点在X轴上，则a等于
    3
    2
    3
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•绵阳二模）已知曲线C1：
    x=cosθ
    y=sinθ
    （θ为参数）和曲线C2=：x2+y2-2
    		3
    x+2y+3=0義于直线l1对称，直线l2过原点且与l1的夹角为30°，则直线l2的方程为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知曲线C1：
    x=-2+cost
    y=1+sint
     （t为参数），C2：
    x=4cosθ
    y=3sinθ
    （q为参数）．
    （Ⅰ）化C1，C2的方程为普通方程，并说明它们分别表示什么曲线；
    （Ⅱ）过曲线C2的左顶点且倾斜角为
    π
    4
    的直线l交曲绒C1于A，B两点，求|AB|．

    查看答案和解析>>

    同步练习册答案