[题目]在平面直角坐标系xOy中.过点P作圆x2+y2﹣2ax+2y﹣1=0的两条切线.切点分别为M(x1 . y1).N(x2 . y2).且 + =0.则实数a的值为．题目和参考答案——青夏教育精英家教网—

【题目】在平面直角坐标系xOy中，过点P（﹣5，a）作圆x2+y2﹣2ax+2y﹣1=0的两条切线，切点分别为M（x1 ， y1），N（x2 ， y2），且 + =0，则实数a的值为．

【答案】3或﹣2
【解析】解：设MN中点为Q（x0 ， y0），T（1，0），圆心R（a，﹣1），根据对称性，MN⊥PR，
= = = ，
∵kMN= ， + =0
∴kMNkTQ=﹣1，
∴MN⊥TQ，
∴P，Q，R，T共线，
∴kPT=kRT ，
即，
∴a2﹣a﹣6=0，
∴a=3或﹣2．
故答案为：3或﹣2．
两者的和实质上是一个斜率与另一个斜率的倒数和，进而可得两斜率乘积为﹣1，可得P，Q，R，T共线，即可求出实数a的值．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在下列结论中： ①函数y=sin（kπ﹣x）（k∈Z）为奇函数；
②函数的图象关于点对称；
③函数的图象的一条对称轴为 π；
④若tan（π﹣x）=2，则cos2x= ．
其中正确结论的序号为（把所有正确结论的序号都填上）．

查看答案和解析>>

科目：高中数学 来源： 题型：

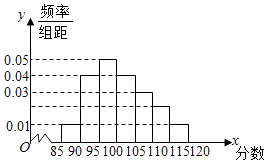
【题目】某校高二奥赛班N名学生的物理测评成绩（满分120分）分布直方图如图，已知分数在100～110的学生数有21人．（Ⅰ）求总人数N和分数在110～115分的人数n；
（Ⅱ）现准备从分数在110～115分的n名学生（女生占）中任选2人，求其中恰好含有一名女生的概率；
（Ⅲ）为了分析某个学生的学习状态，对其下一阶段的学习提供指导性建议，对他前7次考试的数学成绩x（满分150分），物理成绩y进行分析，下面是该生7次考试的成绩．

数学	88	83	117	92	108	100	112
物理	94	91	108	96	104	101	106

已知该生的物理成绩y与数学成绩x是线性相关的，若该生的数学成绩达到130分，请你估计他的物理成绩大约是多少？
附：对于一组数据（u1 ， v1），（u2 ， v2），，（un ， vn），其回归线v=α+βu的斜率和截距的最小二乘估计分别为．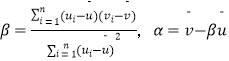

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】若曲线C1：x2+y2﹣2x=0与曲线C2：mx2﹣xy+mx=0有三个不同的公共点，则实数m的取值范围是（）
A.（﹣ ，）
B.（﹣∞，﹣ ）∪（，+∞）
C.（﹣∞，0）∪（0，+∞）
D.（﹣ ，0）∪（0，）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】若圆C1：x2+y2=m与圆C2：x2+y2﹣6x﹣8y+16=0外切．（Ⅰ）求实数m的值；
（Ⅱ）若圆C1与x轴的正半轴交于点A，与y轴的正半轴交于点B，P为第三象限内一点，且点P在圆C1上，直线PA与y轴交于点M，直线PB与x轴交于点N，求证：四边形ABNM的面积为定值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在平面直角坐标系xOy中，已知以M为圆心的圆M：x2+y2﹣12x﹣14y+60=0及其上一点A（2，4）．
（1）设圆N与x轴相切，与圆M外切，且圆心N在直线x=6上，求圆N的标准方程；
（2）设平行于OA的直线l与圆M相交于B、C两点，且BC=OA，求直线l的方程；
（3）设点T（t，0）满足：存在圆M上的两点P和Q，使得 + = ，求实数t的取值范围．