
数列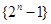 的前
的前 项组成集合
项组成集合 ,从集合
,从集合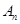 中任取
中任取 个数,其所有可能的
个数,其所有可能的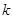 个数的乘积的和为
个数的乘积的和为 (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记 .例如:当
.例如:当 时,
时, ,
, ,
, ;当
;当 时,
时, ,
, ,
, .
.
(Ⅰ)求 ;
;
(Ⅱ)猜想 ,并用数学归纳法证明.
,并用数学归纳法证明.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:解答题
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.
(1)sin213°+cos217°-sin 13°cos 17°.
(2)sin215°+cos215°-sin 15°cos 15°.
(3)sin218°+cos212°-sin 18°cos 12°.
(4)sin2(-18°)+cos248°-sin(-18°)cos 48°.
(5)sin2(-25°)+cos255°-sin(-25°)cos 55°.
①试从上述五个式子中选择一个,求出这个常数.
②根据①的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知多项式f(n)= n5+
n5+ n4+
n4+ n3-
n3- n.
n.
(1)求f(-1)及f(2)的值;
(2)试探求对一切整数n,f(n)是否一定是整数?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com