Question

如果两个相交平面都垂直于第三个平面，那么它们的交线垂直于第三个平面.

已知α⊥γ,β⊥γ,α∩β=l.

求证：l⊥γ.

Answer 1

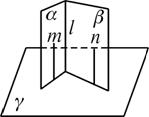
【探究一】在γ内取一点P，作PA垂直α与γ的交线于A，PB垂直β与γ的交线于B，则PA⊥α,PB⊥β.

∵l=α∩β,

∴l⊥PA,l⊥PB.

∵α与β相交，

∴PA与PB相交.

又PAγ,PBγ,∴l⊥γ.

【探究二】在α内作直线m垂直于α与γ的交线，在β内作直线n垂直于β与γ的交线，

∵α⊥γ,β⊥γ,

∴m⊥γ,n⊥γ.

∴m∥n.又nβ,

∴m∥β.∴m∥l,∴l⊥γ.

【探究三】在l上取一点P，过点P作γ的垂线l′,

.

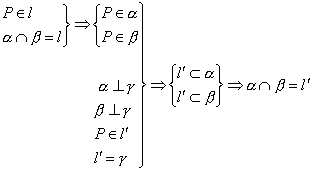但α∩β=l,∴l与l′重合.

∴l⊥γ.

【规律总结】 探究一、探究二都是利用“两平面垂直时，在一个平面内垂直于两平面的交线的直线垂直于另一个平面”这一性质，添加了在一个平面内垂直于交线的直线这样的辅助线.这是两种证法的关键.

    探究三是利用“如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线，在第一个平面内”这一性质，添加了l′这条辅助线，这是关键.

    通过此例，应仔细体会两平面垂直时，添加辅助线的方法.